Fisher transformation

Short description: Statistical transformation

A graph of the transformation (in orange). The untransformed sample correlation coefficient is plotted on the horizontal axis, and the transformed coefficient is plotted on the vertical axis. The identity function (gray) is also shown for comparison.

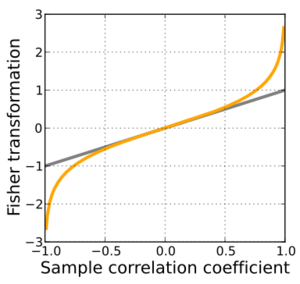
In statistics, the Fisher transformation (or Fisher z-transformation) of a Pearson correlation coefficient is its inverse hyperbolic tangent (artanh). When the sample correlation coefficient r is near 1 or -1, its distribution is highly skewed, which makes it difficult to estimate confidence intervals and apply tests of significance for the population correlation coefficient ρ. The Fisher transformation solves this problem by yielding a variable whose distribution is approximately normally distributed, with a variance that is stable over different values of r.

Definition

Given a set of N bivariate sample pairs (X_i, Y_i), i = 1, …, N, the sample correlation coefficient r is given by

[math]\displaystyle{ r = \frac{\operatorname{cov}(X,Y)}{\sigma_X \sigma_Y} = \frac{\sum ^N _{i=1}(X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum ^N _{i=1}(X_i - \bar{X})^2} \sqrt{\sum ^N _{i=1}(Y_i - \bar{Y})^2}}. }[/math]

Here [math]\displaystyle{ \operatorname{cov}(X,Y) }[/math] stands for the covariance between the variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ \sigma }[/math] stands for the standard deviation of the respective variable. Fisher's z-transformation of r is defined as

[math]\displaystyle{ z = {1 \over 2}\ln\left({1+r \over 1-r}\right) = \operatorname{artanh}(r), }[/math]

where "ln" is the natural logarithm function and "artanh" is the inverse hyperbolic tangent function.

If (X, Y) has a bivariate normal distribution with correlation ρ and the pairs (X_i, Y_i) are independent and identically distributed, then z is approximately normally distributed with mean

[math]\displaystyle{ {1 \over 2}\ln\left({{1+\rho} \over {1-\rho}}\right), }[/math]

and standard error

[math]\displaystyle{ {1 \over \sqrt{N-3}}, }[/math]

where N is the sample size, and ρ is the true correlation coefficient.

This transformation, and its inverse

[math]\displaystyle{ r = \frac{\exp(2z)-1}{\exp(2z)+1} = \operatorname{tanh}(z), }[/math]

can be used to construct a large-sample confidence interval for r using standard normal theory and derivations. See also application to partial correlation.

Derivation

Fisher Transformation with [math]\displaystyle{ \rho =0.9 }[/math] and [math]\displaystyle{ N=30 }[/math]. Illustrated is the exact probability density function of [math]\displaystyle{ r }[/math] (in black), together with the probability density functions of the usual Fisher transformation (blue) and that obtained by including extra terms that depend on [math]\displaystyle{ N }[/math] (red). The latter approximation is visually indistinguishable from the exact answer (its maximum error is 0.3%, compared to 3.4% of basic Fisher).

Hotelling gives a concise derivation of the Fisher transformation.

To derive the Fisher transformation, one starts by considering an arbitrary increasing, twice-differentiable function of [math]\displaystyle{ r }[/math], say [math]\displaystyle{ G(r) }[/math]. Finding the first term in the large-[math]\displaystyle{ N }[/math] expansion of the corresponding skewness [math]\displaystyle{ \kappa_3 }[/math] results in

[math]\displaystyle{ \kappa_3=\frac{6\rho -3(1-\rho ^{2})G^{\prime \prime }(\rho )/G^{\prime }(\rho )}{\sqrt{N}}+O(N^{-3/2}). }[/math]

Setting [math]\displaystyle{ \kappa_3=0 }[/math] and solving the corresponding differential equation for [math]\displaystyle{ G }[/math] yields the inverse hyperbolic tangent [math]\displaystyle{ G(\rho)=\operatorname{artanh}(\rho) }[/math] function.

Similarly expanding the mean m and variance v of [math]\displaystyle{ \operatorname{artanh}(r) }[/math], one gets

m = [math]\displaystyle{ \operatorname{artanh}(\rho )+\frac{\rho }{2N}+O(N^{-2}) }[/math]

and

v = [math]\displaystyle{ \frac{1}{N}+\frac{6-\rho ^{2}}{2N^{2}}+O(N^{-3}) }[/math]

respectively.

The extra terms are not part of the usual Fisher transformation. For large values of [math]\displaystyle{ \rho }[/math] and small values of [math]\displaystyle{ N }[/math] they represent a large improvement of accuracy at minimal cost, although they greatly complicate the computation of the inverse – a closed-form expression is not available. The near-constant variance of the transformation is the result of removing its skewness – the actual improvement is achieved by the latter, not by the extra terms. Including the extra terms, i.e., computing (z-m)/v^1/2, yields:

[math]\displaystyle{ \frac{z-\operatorname{artanh}(\rho )-\frac{\rho }{2N}}{\sqrt{\frac{1}{N}+\frac{6-\rho ^{2}}{2N^{2}}}} }[/math]

which has, to an excellent approximation, a standard normal distribution.

Calculator for the confidence belt of r-squared values (or coefficient of determination/explanation or goodness of fit).

Application

The application of Fisher's transformation can be enhanced using a software calculator as shown in the figure. Assuming that the r-squared value found is 0.80, that there are 30 data, and accepting a 90% confidence interval, the r-squared value in another random sample from the same population may range from 0.588 to 0.921. When r-squared is outside this range, the population is considered to be different. However, if a certain data set is analysed with two different regression models while the first model yields r-squared = 0.80 and the second r-squared is 0.49, one may conclude that the second model is insignificant as the value 0.49 is below the critical value 0.588.

Discussion

The Fisher transformation is an approximate variance-stabilizing transformation for r when X and Y follow a bivariate normal distribution. This means that the variance of z is approximately constant for all values of the population correlation coefficient ρ. Without the Fisher transformation, the variance of r grows smaller as |ρ| gets closer to 1. Since the Fisher transformation is approximately the identity function when |r| < 1/2, it is sometimes useful to remember that the variance of r is well approximated by 1/N as long as |ρ| is not too large and N is not too small. This is related to the fact that the asymptotic variance of r is 1 for bivariate normal data.

The behavior of this transform has been extensively studied since Fisher introduced it in 1915. Fisher himself found the exact distribution of z for data from a bivariate normal distribution in 1921; Gayen in 1951 determined the exact distribution of z for data from a bivariate Type A Edgeworth distribution. Hotelling in 1953 calculated the Taylor series expressions for the moments of z and several related statistics and Hawkins in 1989 discovered the asymptotic distribution of z for data from a distribution with bounded fourth moments.

An alternative to the Fisher transformation is to use the exact confidence distribution density for ρ given by [math]\displaystyle{ \pi (\rho | r) = \frac{\Gamma(\nu+1)}{\sqrt{2\pi}\Gamma(\nu + \frac{1}{2})} (1 - r^2)^{\frac{\nu - 1}{2}} \cdot (1 - \rho^2)^{\frac{\nu - 2}{2}} \cdot (1 - r \rho )^{\frac{1-2\nu}{2}} F\!\left(\frac{3}{2},-\frac{1}{2}; \nu + \frac{1}{2}; \frac{1 + r \rho}{2}\right) }[/math] where [math]\displaystyle{ F }[/math] is the Gaussian hypergeometric function and [math]\displaystyle{ \nu = N-1 \gt 1 }[/math] .

Other uses

While the Fisher transformation is mainly associated with the Pearson product-moment correlation coefficient for bivariate normal observations, it can also be applied to Spearman's rank correlation coefficient in more general cases. A similar result for the asymptotic distribution applies, but with a minor adjustment factor: see the cited article for details.

See also

• Data transformation (statistics)
• Meta-analysis (this transformation is used in meta analysis for stabilizing the variance)
• Partial correlation
• Pearson correlation coefficient § Inference

External links

• R implementation