Skewed generalized t distribution

Short description: Family of continuous probability distributions

In probability and statistics, the skewed generalized "t" distribution is a family of continuous probability distributions. The distribution was first introduced by Panayiotis Theodossiou in 1998. The distribution has since been used in different applications. There are different parameterizations for the skewed generalized t distribution.

Definition

Probability density function

[math]\displaystyle{ f_\text{SGT}(x; \mu, \sigma, \lambda, p, q) = \frac{p}{2 v \sigma q^{\frac{1}{p}} B(\frac{1}{p},q) \left[1 + \frac{| x-\mu + m |^p}{q (v \sigma)^p (1 + \lambda \sgn(x-\mu + m))^p}\right]^{\frac{1}{p}+q}} }[/math]

where [math]\displaystyle{ B }[/math] is the beta function, [math]\displaystyle{ \mu }[/math] is the location parameter, [math]\displaystyle{ \sigma \gt 0 }[/math] is the scale parameter, [math]\displaystyle{ -1 \lt \lambda \lt 1 }[/math] is the skewness parameter, and [math]\displaystyle{ p \gt 0 }[/math] and [math]\displaystyle{ q \gt 0 }[/math] are the parameters that control the kurtosis. [math]\displaystyle{ m }[/math] and [math]\displaystyle{ v }[/math] are not parameters, but functions of the other parameters that are used here to scale or shift the distribution appropriately to match the various parameterizations of this distribution.

In the original parameterization of the skewed generalized t distribution,

[math]\displaystyle{ m = \lambda v \sigma \frac{2 q^{\frac{1}{p}} B(\frac{2}{p},q-\frac{1}{p})}{B(\frac{1}{p},q)} }[/math]

and

[math]\displaystyle{ v = \frac{q^{-\frac{1}{p}}}{\sqrt{ (1 + 3 \lambda^2) \frac{ B ( \frac{3}{p}, q - \frac{2}{p} )}{B (\frac{1}{p}, q )} -4 \lambda^2 \frac{B ( \frac{2}{p}, q - \frac{1}{p} )^2}{ B (\frac{1}{p}, q )^2}}} }[/math].

These values for [math]\displaystyle{ m }[/math] and [math]\displaystyle{ v }[/math] yield a distribution with mean of [math]\displaystyle{ \mu }[/math] if [math]\displaystyle{ pq \gt 1 }[/math] and a variance of [math]\displaystyle{ \sigma^2 }[/math] if [math]\displaystyle{ pq \gt 2 }[/math]. In order for [math]\displaystyle{ m }[/math] to take on this value however, it must be the case that [math]\displaystyle{ pq \gt 1 }[/math]. Similarly, for [math]\displaystyle{ v }[/math] to equal the above value, [math]\displaystyle{ pq \gt 2 }[/math].

The parameterization that yields the simplest functional form of the probability density function sets [math]\displaystyle{ m = 0 }[/math] and [math]\displaystyle{ v = 1 }[/math]. This gives a mean of

[math]\displaystyle{ \mu+ \frac{2 v \sigma \lambda q^{\frac{1}{p}} B(\frac{2}{p},q-\frac{1}{p})}{B(\frac{1}{p},q)} }[/math]

and a variance of

[math]\displaystyle{ \sigma^2 q^{\frac{2}{p}} ( (1 + 3 \lambda^2) \frac{ B ( \frac{3}{p}, q - \frac{2}{p} )}{B (\frac{1}{p}, q )} -4 \lambda^2 \frac{B ( \frac{2}{p}, q - \frac{1}{p} )^2}{ B (\frac{1}{p}, q )^2}) }[/math]

The [math]\displaystyle{ \lambda }[/math] parameter controls the skewness of the distribution. To see this, let [math]\displaystyle{ M }[/math] denote the mode of the distribution, and

[math]\displaystyle{ \int_{-\infty}^{M} f_\text{SGT}(x; \mu, \sigma, \lambda, p, q) \mathrm{d}x = \frac{1-\lambda}{2} }[/math]

Since [math]\displaystyle{ -1 \lt \lambda \lt 1 }[/math], the probability left of the mode, and therefore right of the mode as well, can equal any value in (0,1) depending on the value of [math]\displaystyle{ \lambda }[/math]. Thus the skewed generalized t distribution can be highly skewed as well as symmetric. If [math]\displaystyle{ -1 \lt \lambda \lt 0 }[/math], then the distribution is negatively skewed. If [math]\displaystyle{ 0 \lt \lambda \lt 1 }[/math], then the distribution is positively skewed. If [math]\displaystyle{ \lambda = 0 }[/math], then the distribution is symmetric.

Finally, [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] control the kurtosis of the distribution. As [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] get smaller, the kurtosis increases (i.e. becomes more leptokurtic). Large values of [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] yield a distribution that is more platykurtic.

Moments

Let [math]\displaystyle{ X }[/math] be a random variable distributed with the skewed generalized t distribution. The [math]\displaystyle{ h^{th} }[/math] moment (i.e. [math]\displaystyle{ E[(X- E(X))^h] }[/math]), for [math]\displaystyle{ pq \gt h }[/math], is: [math]\displaystyle{ \sum_{r=0}^{h} \binom{h}{r} ((1+\lambda)^{r+1}+(-1)^r (1-\lambda)^{r+1} ) ( - \lambda )^{h-r} \frac{ (v \sigma)^h q^{\frac{h}{p}} B(\frac{r+1}{p},q-\frac{r}{p}) B(\frac{2}{p},q-\frac{1}{p} )^{h-r}}{ 2^{r-h+1} B(\frac{1}{p},q)^{h-r+1} } }[/math]

The mean, for [math]\displaystyle{ pq \gt 1 }[/math], is:

[math]\displaystyle{ \mu + \frac{2 v \sigma \lambda q^{\frac{1}{p}} B(\frac{2}{p},q-\frac{1}{p})}{B(\frac{1}{p},q)} - m }[/math]

The variance (i.e. [math]\displaystyle{ E[(X- E(X))^2] }[/math]), for [math]\displaystyle{ pq \gt 2 }[/math], is:

[math]\displaystyle{ (v \sigma)^2 q^{\frac{2}{p}} ( (1 + 3 \lambda^2) \frac{ B ( \frac{3}{p}, q - \frac{2}{p} )}{B (\frac{1}{p}, q )} -4 \lambda^2 \frac{B ( \frac{2}{p}, q - \frac{1}{p} )^2}{ B (\frac{1}{p}, q )^2}) }[/math]

The skewness (i.e. [math]\displaystyle{ E[(X- E(X))^3] }[/math]), for [math]\displaystyle{ pq \gt 3 }[/math], is:

[math]\displaystyle{ \frac{2 q^{3/p} \lambda (v \sigma) ^3}{B(\frac{1}{p},q)^3} \Bigg( 8 \lambda ^2 B(\frac{2}{p},q-\frac{1}{p})^3-3 (1+3 \lambda ^2) B(\frac{1}{p},q) }[/math]

[math]\displaystyle{ \times B(\frac{2}{p},q-\frac{1}{p}) B(\frac{3}{p},q-\frac{2}{p})+2 (1+\lambda ^2) B(\frac{1}{p},q)^2 B(\frac{4}{p},q-\frac{3}{p}) \Bigg) }[/math]

The kurtosis (i.e. [math]\displaystyle{ E[(X- E(X))^4] }[/math]), for [math]\displaystyle{ pq \gt 4 }[/math], is:

[math]\displaystyle{ \frac{q^{4/p} (v \sigma) ^4}{B(\frac{1}{p},q)^4} \Bigg( -48 \lambda ^4 B(\frac{2}{p},q-\frac{1}{p})^4+24 \lambda ^2 (1+3 \lambda ^2) B(\frac{1}{p},q) B(\frac{2}{p},q-\frac{1}{p})^2 }[/math]

[math]\displaystyle{ \times B(\frac{3}{p},q-\frac{2}{p})-32 \lambda ^2 (1+\lambda ^2) B(\frac{1}{p},q)^2 B(\frac{2}{p},q-\frac{1}{p}) B(\frac{4}{p},q-\frac{3}{p}) }[/math]

[math]\displaystyle{ +(1+10 \lambda ^2+5 \lambda ^4) B(\frac{1}{p},q)^3 B(\frac{5}{p},q-\frac{4}{p})\Bigg) }[/math]

Special Cases

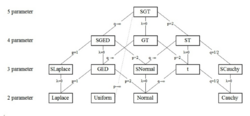
Special and limiting cases of the skewed generalized t distribution include the skewed generalized error distribution, the generalized t distribution introduced by McDonald and Newey, the skewed t proposed by Hansen, the skewed Laplace distribution, the generalized error distribution (also known as the generalized normal distribution), a skewed normal distribution, the student t distribution, the skewed Cauchy distribution, the Laplace distribution, the uniform distribution, the normal distribution, and the Cauchy distribution. The graphic below, adapted from Hansen, McDonald, and Newey, shows which parameters should be set to obtain some of the different special values of the skewed generalized t distribution.

The skewed generalized t distribution tree

Skewed generalized error distribution

The Skewed Generalized Error Distribution (SGED) has the pdf:

[math]\displaystyle{ \lim_{q\to\infty} f_\text{SGT}(x; \mu, \sigma, \lambda, p, q) }[/math]

[math]\displaystyle{ = f_\text{SGED}(x; \mu, \sigma, \lambda, p) = \frac{p}{2 v \sigma \Gamma ( \frac{1}{p} )} e^{- \left( \frac{|x - \mu + m|}{ v \sigma [1 + \lambda \sgn(x - \mu + m)]} \right)^p } }[/math]

where

[math]\displaystyle{ m = \lambda v \sigma \frac{ 2^{ \frac{2}{p} } \Gamma ( \frac{1}{2} + \frac{1}{p} ) }{ \sqrt{\pi}} }[/math]

gives a mean of [math]\displaystyle{ \mu }[/math]. Also

[math]\displaystyle{ v = \sqrt{\frac{\pi \Gamma(\frac{1}{p})}{ \pi (1+3 \lambda ^2) \Gamma( \frac{3}{p})-16^{\frac{1}{p}} \lambda ^2 \Gamma(\frac{1}{2}+\frac{1}{p})^2 \Gamma(\frac{1}{p})}} }[/math]

gives a variance of [math]\displaystyle{ \sigma^2 }[/math].

Generalized t-distribution

The generalized t-distribution (GT) has the pdf:

[math]\displaystyle{ f_\text{SGT}(x; \mu, \sigma, \lambda{=}0, p, q) }[/math]

[math]\displaystyle{ = f_\text{GT}(x; \mu, \sigma, p, q) = \frac{p}{2 v \sigma q^{\frac{1}{p}} B(\frac{1}{p},q) \left[1 + \frac{\left| x-\mu \right| ^p}{q (v \sigma) ^p }\right]^{\frac{1}{p}+q}} }[/math]

where

[math]\displaystyle{ v = \frac{1}{q^{\frac{1}{p}}} \sqrt{\frac{ B(\frac{1}{p},q) }{ B(\frac{3}{p},q-\frac{2}{p}) }} }[/math]

gives a variance of [math]\displaystyle{ \sigma^2 }[/math].

Skewed t-distribution

The skewed t-distribution (ST) has the pdf:

[math]\displaystyle{ f_\text{SGT}(x; \mu, \sigma, \lambda, p{=}2, q) }[/math]

[math]\displaystyle{ = f_\text{ST}(x; \mu, \sigma, \lambda, q) = \frac{\Gamma ( \frac{1}{2}+q )}{v \sigma (\pi q)^{\frac{1}{2}} \Gamma (q) \left[ 1 + \frac{\left| x-\mu + m \right| ^2}{q (v \sigma) ^2 (1+\lambda \sgn(x-\mu + m))^2}\right]^{\frac{1}{2}+q}} }[/math]

where

[math]\displaystyle{ m = \lambda v \sigma \frac{2 q^{\frac{1}{2}} \Gamma (q-\frac{1}{2})}{\pi^{\frac{1}{2}} \Gamma (q)} }[/math]

gives a mean of [math]\displaystyle{ \mu }[/math]. Also

[math]\displaystyle{ v = \frac{1}{q^{\frac{1}{2}} \sqrt{ (1 + 3 \lambda^2) \frac{1}{2q-2} -\frac{4 \lambda^2}{\pi} \left( \frac{\Gamma ( q - \frac{1}{2} )}{ \Gamma ( q )} \right)^2 }} }[/math]

gives a variance of [math]\displaystyle{ \sigma^2 }[/math].

Skewed Laplace distribution

The skewed Laplace distribution (SLaplace) has the pdf:

[math]\displaystyle{ \lim_{q\to\infty} f_\text{SGT}(x; \mu, \sigma, \lambda, p{=}1, q) }[/math]

[math]\displaystyle{ = f_\text{SLaplace}(x; \mu, \sigma, \lambda) = \frac{1}{2 v \sigma} e^{- \frac{ |x - \mu + m|}{ v \sigma (1 + \lambda \sgn(x - \mu + m))} } }[/math]

where

[math]\displaystyle{ m = 2 v \sigma \lambda }[/math]

gives a mean of [math]\displaystyle{ \mu }[/math]. Also

[math]\displaystyle{ v = [ 2 (1+\lambda ^2) ]^{-\frac{1}{2}} }[/math]

gives a variance of [math]\displaystyle{ \sigma^2 }[/math].

Generalized error distribution

The generalized error distribution (GED, also known as the generalized normal distribution) has the pdf:

[math]\displaystyle{ \lim_{q\to\infty} f_\text{SGT}(x; \mu, \sigma, \lambda{=}0, p, q) }[/math]

[math]\displaystyle{ = f_\text{GED}(x; \mu, \sigma, p) = \frac{p}{2 v \sigma \Gamma ( \frac{1}{p} )} e^{- \left( \frac{|x - \mu|}{ v \sigma} \right)^p } }[/math]

where

[math]\displaystyle{ v = \sqrt{ \frac{\Gamma ( \frac{1}{p} )}{ \Gamma ( \frac{3}{p} )}} }[/math]

gives a variance of [math]\displaystyle{ \sigma^2 }[/math].

Skewed normal distribution

The skewed normal distribution (SNormal) has the pdf:

[math]\displaystyle{ \lim_{q\to\infty} f_\text{SGT}(x; \mu, \sigma, \lambda, p{=}2, q) }[/math]

[math]\displaystyle{ = f_\text{SNormal}(x; \mu, \sigma, \lambda) = \frac{1}{v \sigma \sqrt{\pi}} e^{- \left[ \frac{|x - \mu + m|}{ v \sigma (1 + \lambda \sgn(x - \mu + m))} \right]^2 } }[/math]

where

[math]\displaystyle{ m = \lambda v \sigma \frac{ 2 }{ \sqrt{\pi}} }[/math]

gives a mean of [math]\displaystyle{ \mu }[/math]. Also

[math]\displaystyle{ v = \sqrt{\frac{2 \pi }{ \pi -8 \lambda ^2+3 \pi \lambda ^2} } }[/math]

gives a variance of [math]\displaystyle{ \sigma^2 }[/math].

The distribution should not be confused with the skew normal distribution or another asymmetric version. Indeed, the distribution here is a special case of a bi-Gaussian, whose left and right widths are proportional to [math]\displaystyle{ 1-\lambda }[/math] and [math]\displaystyle{ 1+\lambda }[/math].

Student's t-distribution

The Student's t-distribution (T) has the pdf:

[math]\displaystyle{ f_\text{SGT}(x; \mu{=}0, \sigma{=}1, \lambda{=}0, p{=}2, q{=}\tfrac{d}{2}) }[/math]

[math]\displaystyle{ = f_\text{T}(x; d) = \frac{\Gamma ( \frac{d+1}{2} )}{ (\pi d)^{\frac{1}{2}} \Gamma (\frac{d}{2})} \left(1 + \frac{x^2}{d}\right)^{-\frac{d+1}{2}} }[/math]

[math]\displaystyle{ v = \sqrt{2} }[/math] was substituted.

Skewed Cauchy distribution

The skewed cauchy distribution (SCauchy) has the pdf:

[math]\displaystyle{ f_\text{SGT}(x; \mu, \sigma, \lambda, p{=}2, q{=}\tfrac{1}{2}) }[/math]

[math]\displaystyle{ = f_\text{SCauchy}(x; \mu, \sigma, \lambda) = \frac{1}{\sigma \pi \left[1 + \frac{\left| x-\mu \right| ^2}{ \sigma ^2 (1+\lambda \sgn(x-\mu ))^2}\right]} }[/math]

[math]\displaystyle{ v = \sqrt{2} }[/math] and [math]\displaystyle{ m = 0 }[/math] was substituted.

The mean, variance, skewness, and kurtosis of the skewed Cauchy distribution are all undefined.

Laplace distribution

The Laplace distribution has the pdf:

[math]\displaystyle{ \lim_{q\to\infty} f_\text{SGT}(x; \mu, \sigma, \lambda{=}0, p{=}1, q) }[/math]

[math]\displaystyle{ = f_\text{Laplace}(x; \mu, \sigma) = \frac{1}{2 \sigma } e^{ -\frac{|x - \mu|}{ \sigma } } }[/math]

[math]\displaystyle{ v = 1 }[/math] was substituted.

Uniform Distribution

The uniform distribution has the pdf:

[math]\displaystyle{ \lim_{p\to\infty} f_\text{SGT}(x; \mu, \sigma, \lambda, p, q) }[/math]

[math]\displaystyle{ = f(x)=\begin{cases} \frac{1}{2 v \sigma} & |x - \mu| \lt v \sigma \\ 0 & \mathrm{otherwise} \end{cases} }[/math]

Thus the standard uniform parameterization is obtained if [math]\displaystyle{ \mu = \frac{a+b}{2} }[/math], [math]\displaystyle{ v = 1 }[/math], and [math]\displaystyle{ \sigma = \frac{b-a}{2} }[/math].

Normal distribution

The normal distribution has the pdf:

[math]\displaystyle{ \lim_{q\to\infty} f_\text{SGT}(x; \mu, \sigma, \lambda{=}0, p{=}2, q) }[/math]

[math]\displaystyle{ = f_\text{Normal}(x; \mu, \sigma) = \frac{e^{- \left( \frac{|x - \mu|}{ v \sigma } \right)^2 }}{v \sigma \sqrt{\pi}} }[/math]

where

[math]\displaystyle{ v = \sqrt{2} }[/math]

gives a variance of [math]\displaystyle{ \sigma^2 }[/math].

Cauchy Distribution

The Cauchy distribution has the pdf:

[math]\displaystyle{ f_\text{SGT}(x; \mu, \sigma, \lambda{=}0, p{=}2, q{=}\tfrac{1}{2}) }[/math]

[math]\displaystyle{ = f_\text{Cauchy}(x; \mu, \sigma) = \frac{1}{ \sigma \pi \left[1 + \left( \frac{x- \mu}{\sigma} \right)^2\right]} }[/math]

[math]\displaystyle{ v = \sqrt{2} }[/math] was substituted.

References

• Hansen, B. (1994). "Autoregressive Conditional Density Estimation". International Economic Review 35 (3): 705–730. doi:10.2307/2527081. 
• Hansen, C.; McDonald, J.; Newey, W. (2010). "Instrumental Variables Estimation with Flexible Distributions". Journal of Business and Economic Statistics 28: 13–25. doi:10.1198/jbes.2009.06161. 
• Hansen, C.; McDonald, J.; Theodossiou, P. (2007). "Some Flexible Parametric Models for Partially Adaptive Estimators of Econometric Models". Economics: The Open-Access, Open-Assessment e-Journal 1 (2007–7): 1. doi:10.5018/economics-ejournal.ja.2007-7. 
• McDonald, J.; Michefelder, R.; Theodossiou, P. (2009). "Evaluation of Robust Regression Estimation Methods and Intercept Bias: A Capital Asset Pricing Model Application". Multinational Finance Journal 15 (3/4): 293–321. doi:10.17578/13-3/4-6. http://www.mfsociety.org/modules/modDashboard/uploadFiles/journals/MJ~777~p16uelq1mr19251cptdtu1nab1lsr4.pdf. 
• McDonald, J.; Michelfelder, R.; Theodossiou, P. (2010). "Robust Estimation with Flexible Parametric Distributions: Estimation of Utility Stock Betas". Quantitative Finance 10 (4): 375–387. doi:10.1080/14697680902814241. 
• McDonald, J.; Newey, W. (1988). "Partially Adaptive Estimation of Regression Models via the Generalized t Distribution". Econometric Theory 4 (3): 428–457. doi:10.1017/s0266466600013384. 
• Savva, C.; Theodossiou, P. (2015). "Skewness and the Relation between Risk and Return". Management Science. 
• Theodossiou, P. (1998). "Financial Data and the Skewed Generalized T Distribution". Management Science 44 (12–part–1): 1650–1661. doi:10.1287/mnsc.44.12.1650. 

External links

• outlines skewed generalized t distribution, its special cases, and a program to calculate its pdf, cdf, and critical values
• online demo https://www.desmos.com/calculator/hfb11etkeq