Astronomy:Solar radio emission

From HandWiki
Short description: Radio waves produced by the Sun

Solar radio emission refers to radio waves that are naturally produced by the Sun, primarily from the lower and upper layers of the atmosphere called the chromosphere and corona, respectively. The Sun produces radio emissions through four known mechanisms, each of which operates primarily by converting the energy of moving electrons into electromagnetic radiation. The four emission mechanisms are thermal bremsstrahlung (braking) emission, gyromagnetic emission, plasma emission, and electron-cyclotron maser emission. The first two are incoherent mechanisms, which means that they are the summation of radiation generated independently by many individual particles. These mechanisms are primarily responsible for the persistent "background" emissions that slowly vary as structures in the atmosphere evolve. The latter two processes are coherent mechanisms, which refers to special cases where radiation is efficiently produced at a particular set of frequencies. Coherent mechanisms can produce much larger brightness temperatures (intensities) and are primarily responsible for the intense spikes of radiation called solar radio bursts, which are byproducts of the same processes that lead to other forms of solar activity like solar flares and coronal mass ejections.

History and observations

A collage of antennas from various low-frequency radio interferometry telescopes used to observe the Sun. From left to right, top to bottom: the Culgoora Radioheliograph, Clark Lake Radioheliograph, Guaribidanur Radioheliograph, Nancay Radioheliograph, Murchison Widefield Array, and Low Frequency Array.

Radio emission from the Sun was first reported in the scientific literature by Grote Reber in 1944.[1] Those were observations of 160 MHz frequency (2 meters wavelength) microwave emission emanating from the chromosphere. However, the earliest known observation was in 1942 during World War II by British radar operators who detected an intense low-frequency solar radio burst; that information was kept secret as potentially useful in evading enemy radar, but was later described in a scientific journal after the war.[2] One of the most significant discoveries from early solar radio astronomers such as Joseph Pawsey was that the Sun produces much more radio emission than expected from standard black body radiation.[3] The explanation for this was proposed by Vitaly Ginzburg in 1946, who suggested that thermal bremsstrahlung emission from a million-degree corona was responsible.[4] The existence of such extraordinarily high temperatures in the corona had previously been indicated by optical spectroscopy observations, but the idea remained controversial until it was later confirmed by the radio data.[5]

Prior to 1950, observations were conducted mainly using antennas that recorded the intensity of the whole Sun at a single radio frequency.[6] Observers such as Ruby Payne-Scott and Paul Wild used simultaneous observations at numerous frequencies to find that the onset times of radio bursts varied depending on frequency, suggesting that radio bursts were related to disturbances that propagate outward, away from the Sun, through different layers of plasma with different densities.[7] These findings motivated the development of radiospectrographs that were capable of continuously observing the Sun over a range of frequencies. This type of observation is called a dynamic spectrum, and much of the terminology used to describe solar radio emission relates to features observed in dynamic spectra, such as the classification of solar radio bursts.[8] Examples of dynamic spectra are shown below in the radio burst section. Notable contemporary solar radiospectrographs include the Radio Solar Telescope Network, the e-CALLISTO network, and the WAVES instrument on-board the Wind spacecraft.

Radiospectrographs do not produce images, however, and so they cannot be used to locate features spatially. This can make it very difficult to understand where a specific component of the solar radio emission is coming from and how it relates to features seen at other wavelengths. Producing a radio image of the Sun requires an interferometer, which in radio astronomy means an array of many telescopes that operate together as a single telescope to produce an image. This technique is a sub-type of interferometry called aperture synthesis. Beginning in the 1950s, a number of simple interferometers were developed that could provide limited tracking of radio bursts.[6] This also included the invention of sea interferometry, which was used to associate radio activity with sunspots.[9]

Routine imaging of the radio Sun began in 1967 with the commissioning of the Culgoora Radioheliograph, which operated until 1986.[10] A radioheliograph is simply an interferometer that is dedicated to observing the Sun. In addition to Culgoora, notable examples include the Clark Lake Radioheliograph,[11] Nançay Radioheliograph, Nobeyama Radioheliograph, Gauribidanur Radioheliograph, Siberian Radioheliograph, and Chinese Spectral Radioheliograph.[12] Additionally, interferometers that are used for other astrophysical observations can also be used to observe the Sun. General-purpose radio telescopes that also perform solar observations include the Very Large Array, Atacama Large Millimeter Array, Murchison Widefield Array, and Low-Frequency Array. The collage above shows antennas from several low-frequency radio telescopes used to observe the Sun.

Mechanisms

All of the processes described below produce radio frequencies that depend on the properties of the plasma where the radiation originates, particularly electron density and magnetic field strength. Two plasma physics parameters are particularly important in this context:

The electron plasma frequency,

[math]\displaystyle{ f_{p} = \sqrt{\frac{e^2n_e}{\pi{}m_e}} \approx 0.009\sqrt{n_e}~\textrm{MHz} }[/math]

 

 

 

 

(1)

and the electron gyrofrequency,

[math]\displaystyle{ f_B = \frac{eB}{2\pi{}m_ec} \approx 2.8B~\textrm{MHz} }[/math]

 

 

 

 

(2)

where [math]\displaystyle{ n_e }[/math] is the electron density in cm−3, [math]\displaystyle{ B }[/math] is the magnetic field strength in Gauss (G), [math]\displaystyle{ e }[/math] is the electron charge, [math]\displaystyle{ m_e }[/math] is the electron mass, and [math]\displaystyle{ c }[/math] is the speed of light. The relative sizes of these two frequencies largely determine which emission mechanism will dominate in a particular environment. For example, high-frequency gyromagnetic emission dominates in the chromosphere, where the magnetic field strengths are comparatively large, whereas low-frequency thermal bremsstrahlung and plasma emission dominates in the corona, where the magnetic field strengths and densities are generally lower than in the chromosphere.[13] In the images below, the first four on the upper left are dominated by gyromagnetic emission from the chromosphere, transition region, and low-corona, while the three images on the right are dominated by thermal bremsstrahlung emission from the corona,[14] with lower frequencies being generated at larger heights above the surface.

Quiet Sun Radio Imaging in Multiple Frequencies
The Sun as seen in radio waves from 25.8 GHz down to 24.6 MHz. From upper-left to lower-right, the observations were recorded by the Nobeyama Radioheliograph (NoRH), Very Large Array (VLA), Nançay Radioheliograph (NRH), Murchison Widefield Array (MWA) and Low-Frequency Array (LOFAR). The solid circles in the images on the right correspond to the size of the Sun seen in visible light.

Thermal bremsstrahlung emission

Bremsstrahlung emission, from the German "braking radiation", refers to electromagnetic waves produced when a charged particle accelerates and some of its kinetic energy is converted into radiation.[15] Thermal bremsstrahlung refers to radiation from a plasma in thermal equilibrium and is primarily driven by Coulomb collisions where an electron is deflected by the electric field of an ion. This is often referred to as free-free emission for a fully ionized plasma like the solar corona because it involves collisions of "free" particles, as opposed to electrons transitioning between bound states in an atom. This is the main source of quiescent background emission from the corona, where quiescent means outside of radio burst periods.[16]

The radio frequency of bremsstrahlung emission is related to a plasma's electron density through the electron plasma frequency ([math]\displaystyle{ f_p }[/math]) from Equation 1.[17] A plasma with a density [math]\displaystyle{ n_e }[/math] can produce emission only at or below the corresponding [math]\displaystyle{ f_p }[/math].[18] Density in the corona generally decreases with height above the visible "surface", or photosphere, meaning that lower-frequency emission is produced higher in the atmosphere, and the Sun appears larger at lower frequencies. This type of emission is most prominent below 300 MHz due to typical coronal densities, but particularly dense structures in the corona and chromosphere can generate bremsstrahlung emission with frequencies into the GHz range.[19]

Gyromagnetic emission

Gyromagnetic emission is also produced from the kinetic energy of a charge particle, generally an electron. However in this case, an external magnetic field causes the particle's trajectory to exhibit a spiral gyromotion, resulting in a centripetal acceleration that in turn produces the electromagnetic waves.[16] Different terminology is used for the same basic phenomenon depending on how fast the particle is spiraling around the magnetic field, which is due to the different mathematics required to describe the physics. Gyroresonance emission refers to slower, non-relativistic speeds and is also called magneto-bremsstrahlung or cyclotron emission. Gyrosynchrotron corresponds to the mildly relativistic case, where the particles rotate at a small but significant fraction of light speed, and synchrotron emission refers to the relativistic case where the speeds approach that of light.

Gyroresonance and gyrosynchrotron are most-important in the solar context, although there may be special cases in which synchrotron emission also operates.[20] For any sub-type, gyromagnetic emission occurs near the electron gyrofrequency ([math]\displaystyle{ f_B }[/math]) from Equation 2 or one of its harmonics. This mechanism dominates when the magnetic field strengths are large such that [math]\displaystyle{ f_B }[/math] > [math]\displaystyle{ f_p }[/math]. This is mainly true in the chromosphere, where gyroresonance emission is the primary source of quiescent (non-burst) radio emission, producing microwave radiation in the GHz range.[13] Gyroresonance emission can also be observed from the densest structures in the corona, where it can be used to measure the coronal magnetic field strength.[21] Gyrosynchrotron emission is responsible for certain types of microwave radio bursts from the chromosphere and is also likely responsible for certain types of coronal radio bursts.[22]

Plasma emission

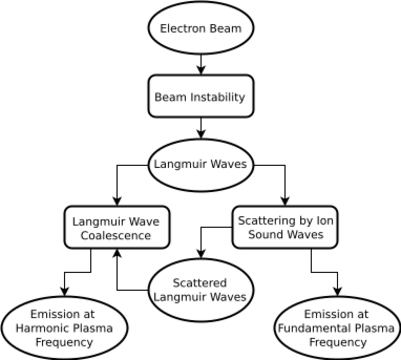
Flowchart outlining the stages of plasma emission, which is responsible for most types of solar radio bursts. In the solar context, the electron beam is accelerated either by magnetic reconnection or a shock wave. Adapted from chart by Donald Melrose[23]

Plasma emission refers to a set of related process that partially convert the energy of Langmuir waves into radiation.[23] It is the most common form of coherent radio emission from the Sun and is commonly accepted as the emission mechanism for most types of solar radio bursts, which can exceed the background radiation level by several orders of magnitude for brief periods.[16] Langmuir waves, also called electron plasma waves or simply plasma oscillations, are electron density oscillations that occur when a plasma is perturbed so that a population of electrons is displaced relative to the ions.[24] Once displaced, the Coloumb force pulls the electrons back toward and ultimately past the ions, leading them to oscillate back and forth.

Langmuir waves are produced in the solar corona by a plasma instability that occurs when a beam of nonthermal (fast-moving) electrons moves through the ambient plasma.[25] The electron beam may be accelerated either by magnetic reconnection, the process that underpins solar flares, or by a shock wave, and these two basic processes operate in different contexts to produce different types of solar radio bursts.[26] The instability that generates Langmuir waves is the two-stream instability, which is also called the beam or bump-on-tail instability in cases such as this where an electron beam is injected into a plasma, creating a "bump" on the high-energy tail of the plasma's particle velocity distribution.[23] This bump facilitates exponential Langmuir wave growth in the ambient plasma through the transfer of energy from the electron beam into specific Langmuir wave modes. A small fraction of the Langmuir wave energy can then be converted into electromagnetic radiation through interactions with other wave modes, namely ion sound waves.[23] A flowchart of the plasma emission stages is shown on the right.

Depending on these wave interactions, coherent radio emission may be produced at the fundamental electron plasma frequency ([math]\displaystyle{ f_p }[/math]; Equation 1) or its harmonic (2[math]\displaystyle{ f_p }[/math]).[27][28] Emission at [math]\displaystyle{ f_p }[/math] is often referred to as fundamental plasma emission, while emission at 2[math]\displaystyle{ f_p }[/math] is called harmonic plasma emission. This distinction is important because the two types have different observed properties and imply different plasma conditions. For example, fundamental plasma emission exhibits a much larger circular polarization fraction[29] and originates from plasma that is four times denser than harmonic plasma emission.[30]

Electron-cyclotron maser emission

The final, and least common, solar radio emission mechanism is electron-cyclotron maser emission (ECME). Maser is an acronym for "microwave amplification by stimulated emission of radiation", which originally referred to a laboratory device that can produce intense radiation of a specific frequency through stimulated emission. Stimulated emission is a process by which a group of atoms are moved into higher energy levels (above thermal equilibrium) and then stimulated to release that extra energy all at once. Such population inversions can occur naturally to produce astrophysical masers, which are sources of very intense radiation of specific spectral lines.[31]

Electron-cyclotron maser emission, however, does not involve population inversions of atomic energy levels.[32] The term maser was adopted here as an analogy is somewhat of a misnomer. In ECME, the injection of nonthermal, semi-relativistic electrons into a plasma produces a population inversion analogous to that of a maser in the sense that a high-energy population was added to an equilibrium distribution. This is very similar to the beginning of the plasma emission process described in the previous section, but when the plasma density is low and/or the magnetic field strength is high such that [math]\displaystyle{ f_B }[/math] > [math]\displaystyle{ f_p }[/math] (Equations 1 and 2), energy from the nonthermal electrons cannot efficiently be converted into Langmuir waves.[32] This leads instead to direct emission at [math]\displaystyle{ f_B }[/math] through a plasma instability that is expressed analytically as a negative absorption coefficient (i.e. positive growth rate) for a particular particle distribution, most famously the loss-cone distribution.[33][23][34] ECME is the accepted mechanism for microwave spike bursts from the chromosphere[16] and is sometimes invoked to explain features of coronal radio bursts that cannot be explained by plasma emission or gyrosynchrotron emission.[35][36]

Magnetoionic theory and polarization

Magnetoionic theory describes the propagation of electromagnetic waves in environments where an ionized plasma is subjected to an external magnetic field, such as the solar corona and Earth's ionosphere.[37][18] The corona is generally treated with the "cold plasma approach," which assumes that the characteristic velocities of the waves are much faster than the thermal velocities of the plasma particles.[17][38] This assumption allows thermal effects to be neglected, and most approaches also ignore the motions of ions and assume that the particles do not interact through collisions.

Under these approximations, the dispersion equation for electromagnetic waves includes two free-space modes that can escape the plasma as radiation (radio waves). These are called the ordinary ([math]\displaystyle{ o }[/math]) and extraordinary ([math]\displaystyle{ x }[/math]) modes.[18] The ordinary mode is "ordinary" in the sense that the plasma response is the same as if there were no magnetic field, while the [math]\displaystyle{ x }[/math]-mode has a somewhat different refractive index. Importantly, each mode is polarized in opposite senses that depend on the angle with respect to the magnetic field. A quasi-circular approximation generally applies, in which case both modes are 100% circularly polarized with opposite senses.[18]

The [math]\displaystyle{ x }[/math]- and [math]\displaystyle{ o }[/math]-modes are produced at different rates depending on the emission mechanism and plasma parameters, which leads to a net circular polarization signal. For example, thermal bremsstrahlung slightly favors the [math]\displaystyle{ x }[/math]-mode, while plasma emission heavily favors the [math]\displaystyle{ o }[/math]-mode.[29] This makes circular polarization an extremely important property for studies of solar radio emission, as it can be used to help understand how the radiation was produced. While circular polarization is most prevalent in solar radio observations, it is also possible to produce linear polarizations in certain circumstances.[39] However, the presence of intense magnetic fields leads to Faraday rotation that distorts linearly-polarized signals, making them extremely difficult or impossible to detect.[40] However, it is possible to detect linearly-polarized background astrophysical sources that are occulted by the corona,[41] in which case the impact of Faraday rotation can be used to measure the coronal magnetic field strength.[42]

Propagation effects

The appearance of solar radio emission, particularly at low frequencies, is heavily influenced by propagation effects.[43] A propagation effect is anything that impacts the path or state of an electromagnetic wave after it is produced. These effects therefore depend on whatever mediums the wave passed through before being observed. The most dramatic impacts to solar radio emission occur in the corona and in Earth's ionosphere. There are three primary effects: refraction, scattering, and mode coupling.

Refraction is the bending of light's path as it enters a new medium or passes through a material with varying density. The density of the corona generally decreases with distance from the Sun, which causes radio waves to refract toward the radial direction.[44][45] When solar radio emission enters Earth's ionosphere, refraction may also severely distort the source's apparent location depending on the viewing angle and ionospheric conditions.[46] The [math]\displaystyle{ x }[/math]- and [math]\displaystyle{ o }[/math]-modes discussed in the previous section also have slightly different refractive indices, which can lead to separation of the two modes.[29]

The counterpart to refraction is reflection. A radio wave can be reflected in the solar atmosphere when it encounters a region of particularly high density compared to where it was produced, and such reflections can occur many times before a radio wave escapes the atmosphere. This process of many successive reflections is called scattering, and it has many important consequences.[47] Scattering increases the apparent size of the entire Sun and compact sources within it, which is called angular broadening.[48][49] Scattering increases the cone-angle over which directed emission can be observed, which can even allow for the observation of low-frequency radio bursts that occurred on the far-side of the Sun.[50] Because the high-density fibers that are primarily responsible for scattering are not randomly aligned and are generally radial, random scattering against them may also systematically shift the observed location of a radio burst to a larger height than where it was actually produced.[51][30] Finally, scattering tends to depolarize emission and is likely why radio bursts often exhibit much lower circular polarization fractions than standard theories predict.[52]

Mode coupling refers to polarization state changes of the [math]\displaystyle{ x }[/math]- and [math]\displaystyle{ o }[/math]-modes in response to different plasma conditions.[53] If a radio wave passes through a region where the magnetic field orientation is nearly perpendicular to the direction of travel, which is called a quasi-transverse region,[54] the polarization sign (i.e. left or right; positive or negative) may flip depending on the radio frequency and plasma parameters.[55] This concept is crucial to interpreting polarization observations of solar microwave radiation[56][57] and may also be important for certain low-frequency radio bursts.[58]

Solar radio bursts

Solar radio bursts are brief periods during which the Sun's radio emission is elevated above the background level.[16] They are signatures of the same processes that lead to the more widely-known forms of solar activity such as sunspots, solar flares, and coronal mass ejections.[17] Radio bursts can exceed the background radiation level only slightly or by several orders of magnitude (e.g. by 10 to 10,000 times) depending on a variety of factors that include the amount of energy released, the plasma parameters of the source region, the viewing geometry, and the mediums through which the radiation propagated before being observed. Most types of solar radio bursts are produced by the plasma emission mechanism operating in different contexts, although some are caused by (gyro)synchrotron and/or electron-cyclotron maser emission.

Solar radio bursts of Types I, II, and III as seen in dynamic spectrum observations from the Learmonth Solar radiospectrograph. The color corresponds to the intensity. The perfectly horizontal features seen at specific frequencies correspond to radio frequency interference from human-generated sources.

Solar radio bursts are classified largely based on how they appear in dynamic spectrum observations from radiospectrographs. The first three types, shown in the image on the right, were defined by Paul Wild and Lindsay McCready in 1950 using the earliest radiospectrograph observations of metric (low-frequency) bursts.[8] This classification scheme is based primarily on how a burst's frequency drifts over time. Types IV and V were added within a few years of the initial three, and a number of other types and sub-types have since been identified.

Type I

Type I bursts are radiation spikes that last around one second and occur over a relatively narrow frequency range ([math]\displaystyle{ \Delta{}f/f \approx 0.025 }[/math]) with little-to-no discernible drift in frequency.[59] They tend to occur in groups called noise storms that are often superimposed on enhanced continuum (broad-spectrum) emission with the same frequency range.[60] While each individual Type I burst does not drift in frequency, a chain of Type I bursts in a noise storm may slowly drift from higher to lower frequencies over a few minutes. Noise storms can last from hours to weeks, and they are generally observed at relatively low frequencies between around 50 and 500 MHz.

Noise storms are associated with active regions.[61] Active regions are regions in the solar atmosphere with high concentrations of magnetic fields, and they include a sunspot at their base in the photosphere except in cases where the magnetic fields are fairly weak.[62] The association with active regions has been known for decades, but the conditions required to produce noise storms are still mysterious. Not all active regions that produce other forms of activity such as flares generate noise storms, and unlike other types of solar radio bursts, it is often difficult to identify non-radio signatures of Type I bursts.[63][64]

The emission mechanism for Type I bursts is generally agreed to be fundamental plasma emission due to the high circular polarization fractions that are frequently observed. However, there is no consensus yet on what process accelerates the electrons needed to stimulate plasma emission. The leading ideas are minor magnetic reconnection events or shock waves driven by upward-propagating waves.[65][66] Since the year 2000, different magnetic reconnection scenarios have generally been favored. One scenario involves reconnection between the open and closed magnetic fields at the boundaries of active regions,[67] and another involves moving magnetic features in the photosphere.[68]

Type II

Type II bursts exhibit a relatively slow drift from high to low frequencies of around 0.05 MHz per second,[69] typically over the course of a few minutes.[70] They often exhibit two distinct bands of emission that correspond to fundamental and harmonic plasma emission emanating from the same region.[71] Type II bursts are associated with coronal mass ejections (CMEs) and are produced at the leading edge of a CME, where a shock wave accelerates the electrons responsible for stimulating plasma emission.[72] The frequency drifts from higher to lower values because it depends on the electron density, and the shock propagates outward away from the Sun through lower and lower densities. By using a model for the Sun's atmospheric density, the frequency drift rate can then be used to estimate the speed of the shock wave. This exercise typically results in speeds of around 1000 km/s, which matches that of CME shocks determined from other methods.[73]

While plasma emission is the accepted mechanism, Type II bursts do not exhibit significant amounts of circular polarization as would be expected by standard plasma emission theory.[74] The reason for this is unknown, but a leading hypothesis is that the polarization level is suppressed by dispersion effects related to having an inhomogeneous magnetic field near a magnetohydrodynamic shock.[75] Type II bursts sometimes exhibit fine structures called herringbone bursts that emanate from the main burst, as it appears in a dynamic spectrum, and extend to lower frequencies. Herringbone structures are believed to result from shock-accelerated electrons that were able to escape far beyond the shock region to excite Langmuir waves in plasma of lower density than the primary burst region.[76][77]

Type III

Like Type II bursts, Type IIIs also drift from high to low frequencies and are widely attributed to the plasma emission mechanism.[78] However, Type III bursts drift much more rapidly, around 100 MHz per second, and must therefore be related to disturbances that move more quickly than the shock waves responsible for Type IIs.[79] Type III bursts are associated with electrons beams that are accelerated to small fractions of light speed ([math]\displaystyle{ \approx }[/math] 0.1 to 0.3 c) by magnetic reconnection, the process responsible for solar flares. In the image below, the chain of color contours show the locations of three Type III bursts at different frequencies. The progression from violet to red corresponds to the trajectories of electron beams moving away from the Sun and exciting lower and lower frequency plasma emission as they encounter lower and lower densities. Given that they are ultimately caused by magnetic reconnection, Type IIIs are strongly associated with X-ray flares and are indeed observed during nearly all large flares.[80] However, small-to-moderate X-ray flares do not always exhibit Type III bursts and vice versa due to the somewhat different conditions that are required for the high- and low-energy emission to be produced and observed.[81][82]

Murchison Widefield Array images of background radiation at 240 MHz (grayscale) with color contours showing Type III bursts at a range of frequencies. The bursts are hundreds of times brighter than the background, and the lower-frequency contours appear at greater heights because the bursts are produced by an electron beam that travels away from the Sun, exciting radio emission of decreasing frequency with increasing distance.

Type III bursts can occur alone, in small groups, or in chains referred to as Type III storms that may last many minutes. They are often subdivided into two types, coronal and interplanetary Type III bursts.[78] Coronal refers to the case for which an electron beam is traveling in the corona within a few solar radii of the photosphere. They typically start at frequencies in the hundreds of MHz and drift down to tens of MHz over a few seconds. The electron beams that excite radiation travel along specific magnetic field lines that may be closed or open to interplanetary space.[83] Electron beams that escape into interplanetary space may excite Langmuir waves in the solar wind plasma to produce interplanetary Type III bursts that can extend down to 20 kHz and below for beams that reach 1 Astronomical Unit and beyond.[78] The very low frequencies of interplanetary bursts are below the ionospheric cutoff ([math]\displaystyle{ \approx }[/math] 10 MHz), meaning they are blocked by Earth's ionosphere and are observable only from space.

Direct, in situ observations of the electrons and Langmuir waves (plasma oscillations) associated with interplanetary Type III bursts are among the most important pieces of evidence for the plasma emission theory of solar radio bursts.[84][85] Type III bursts exhibit moderate levels of circular polarization, typically less than 50%.[86] This is lower than expected from plasma emission and is likely due to depolarization from scattering by density inhomogeneities and other propagation effects.[52]

Type IV

Type IV bursts are spikes of broad-band continuum emission that include a few distinct sub-types associated with different phenomena and different emission mechanisms. The first type to be defined was the moving Type IV burst, which requires imaging observations (i.e. interferometry) to detect.[87] They are characterized by an outward-moving continuum source that is often preceded by a Type II burst in association with a coronal mass ejection (CME).[75] The emission mechanism for Type IV bursts is generally attributed to gyrosynchrotron emission, plasma emission, or some combination of both that results from fast-moving electrons trapped within the magnetic fields of an erupting CME.[16][88]

Stationary Type IV bursts are more common and are not associated with CMEs.[75] They are broad-band continuum emissions associated either with solar flares or Type I bursts.[16] Flare-associated Type IV bursts are also called flare continuum bursts, and they typically begin at or shortly after a flare's impulsive phase. Larger flares often include a storm continuum phase that follows after the flare continuum.[89] The storm continuum can last from hours to days and may transition into an ordinary Type I noise storm in long-duration events.[6] Both flare and storm continuum Type IV bursts are attributed to plasma emission, but the storm continuum exhibits much larger degrees of circular polarization for reasons that are not fully known.[16]

Type V

Type V bursts are the least common of the standard 5 types.[75] They are continuum emissions that last from one to a few minutes immediately after a group of Type III bursts, generally occurring below around 120 MHz.[16] Type Vs are generally thought to be caused by harmonic plasma emission associated with same streams of electrons responsible for the associated Type III bursts.[90] They sometimes exhibit significant positional offsets from the Type III bursts, which may be due to the electrons traveling along somewhat different magnetic field structures.[91] Type V bursts persist for much longer than Type IIIs because they are driven by a slower and less-collimated electron population, which produces broader-band emission and also leads to a reversal in the circular polarization sign from that of the associated Type III bursts due to the different Langmuir wave distribution.[92] While plasma emission is the commonly-accepted mechanism, electron-cyclotron maser emission has also been proposed.[93]

Other types

In addition to the classic five types, there are a number of additional types of solar radio bursts. These include variations of the standard types, fine structure within another type, and entirely distinct phenomena. Variant examples include Types J and U bursts, which are Type III bursts for which the frequency drift reverses to go from lower to higher frequencies, suggesting that an electron beam first traveled away and then back toward the Sun along a closed magnetic field trajectory.[78] Fine structure bursts include zebra patterns[94] and fibre bursts[95] that may be observed within Type IV bursts, along with the herringbone bursts[76] that sometimes accompany Type IIs. Type S bursts, which last only milliseconds, are an example of a distinct class.[96] There are also a variety of high-frequency microwave burst types, such as microwave Type IV bursts, impulsive bursts, postbursts, and spike bursts.[97]

Radio emission from other stars

Due to its proximity to Earth, the Sun is the brightest source of astronomical radio emission. But of course, other stars also produce radio emission and may produce much more intense radiation in absolute terms than is observed from the Sun. For "normal" main sequence stars, the mechanisms that produce stellar radio emission are the same as those that produce solar radio emission.[16] However, emission from "radio stars" may exhibit significantly different properties compared to the Sun, and the relative importance of the different mechanisms may change depending on the properties of the star, particularly with respect to size and rotation rate, the latter of which largely determines the strength of a star's magnetic field. Notable examples of stellar radio emission include quiescent steady emission from stellar chromospheres and coronae, radio bursts from flare stars, radio emission from massive stellar winds, and radio emission associated with close binary stars.[16] Pre-main-sequence stars such as T Tauri stars also exhibit radio emission through reasonably well-understood processes, namely gyrosynchrotron and electron cyclotron maser emission.[98]

Different radio emission processes also exist for certain pre-main-sequence stars, along with post-main sequence stars such as neutron stars.[16] These objects have very high rotation rates, which leads to very intense magnetic fields that are capable of accelerating large amounts of particles to highly-relativistic speeds. Of particular interest is the fact that there is no consensus yet on the coherent radio emission mechanism responsible for pulsars, which cannot be explained by the two well-established coherent mechanisms discussed here, plasma emission and electron cyclotron maser emission.[99] Proposed mechanisms for pulsar radio emission include coherent curvature emission, relativistic plasma emission, anomalous Doppler emission, and linear acceleration emission or free-electron maser emission.[99] All of these processes still involve the transfer of energy from moving electrons into radiation. However, in this case the electrons are moving at nearly the speed of light, and the debate revolves around what process accelerates these electrons and how their energy is converted into radiation.[100]

References

  1. ↑ Reber, Grote (November 1944). "Cosmic Static." (in en). The Astrophysical Journal 100: 279. doi:10.1086/144668. ISSN 0004-637X. Bibcode: 1944ApJ...100..279R. 
  2. ↑ Hey, J. S. (January 1946). "Solar Radiations in the 4–6 Metre Radio Wave-Length Band" (in en). Nature 157 (3976): 47–48. doi:10.1038/157047b0. ISSN 0028-0836. Bibcode: 1946Natur.157...47H. http://www.nature.com/articles/157047b0. 
  3. ↑ Pawsey, J. L. (November 1946). "Observation of Million Degree Thermal Radiation from the Sun at a Wavelength of 1.5 Metres" (in en). Nature 158 (4018): 633–634. doi:10.1038/158633a0. ISSN 0028-0836. Bibcode: 1946Natur.158..633P. http://www.nature.com/articles/158633a0. 
  4. ↑ Ginzburg, Vitaly (1946). "On solar radiation in the radio spectrum". Proceedings (Doklady) of the Academy of Sciences of the USSR 52: 487. 
  5. ↑ Golub, L. (Leon) (2010). The solar corona. Pasachoff, Jay M. (2nd ed.). Cambridge, UK: Cambridge University Press. ISBN 978-0-521-88201-9. OCLC 318870775. https://www.worldcat.org/oclc/318870775. 
  6. ↑ 6.0 6.1 6.2 Pick, Monique; Vilmer, Nicole (2008-10-01). "Sixty-five years of solar radioastronomy: flares, coronal mass ejections and Sun–Earth connection" (in en). The Astronomy and Astrophysics Review 16 (1): 1–153. doi:10.1007/s00159-008-0013-x. ISSN 1432-0754. Bibcode: 2008A&ARv..16....1P. https://doi.org/10.1007/s00159-008-0013-x. 
  7. ↑ Payne-Scott, Ruby; Yabsley, D. E.; Bolton, J. G. (August 1947). "Relative Times of Arrival of Bursts of Solar Noise on Different Radio Frequencies" (in en). Nature 160 (4060): 256–257. doi:10.1038/160256b0. ISSN 0028-0836. PMID 20256214. Bibcode: 1947Natur.160..256P. http://www.nature.com/articles/160256b0. 
  8. ↑ 8.0 8.1 Wild, JP; McCready, LL (1950). "Observatioas of the Spectrum of High-Intensity Solar Radiation at Metre Wavelengths. I. The Apparatus and Spectral Types of Solar Burst Observed". Australian Journal of Chemistry 3 (3): 387. doi:10.1071/ch9500387. ISSN 0004-9425. Bibcode: 1950AuSRA...3..387W. http://dx.doi.org/10.1071/ch9500387. 
  9. ↑ Thompson, A. Richard; Moran, James M.; Swenson, George W. (2001-05-09) (in en). Interferometry and Synthesis in Radio Astronomy (1 ed.). Wiley. doi:10.1002/9783527617845. ISBN 978-0-471-25492-8. https://onlinelibrary.wiley.com/doi/book/10.1002/9783527617845. 
  10. ↑ Wild, J. P. (September 1970). "Some Investigations of the Solar Corona: The First Two Years of Observation With the Culgoora Radioheliograph" (in en). Publications of the Astronomical Society of Australia 1 (8): 365–370. doi:10.1017/S1323358000012364. ISSN 1323-3580. Bibcode: 1970PASA....1..365W. https://www.cambridge.org/core/product/identifier/S1323358000012364/type/journal_article. 
  11. ↑ Kundu, M. R.; Erickson, W. C.; Gergely, T. E.; Mahoney, M. J.; Turner, P. J. (March 1983). "First results from the Clark Lake Multifrequency Radioheliograph" (in en). Solar Physics 83 (2): 385–389. doi:10.1007/BF00148288. ISSN 0038-0938. Bibcode: 1983SoPh...83..385K. http://link.springer.com/10.1007/BF00148288. 
  12. ↑ Wang, Wei; Yan, Yihua; Liu, Fei; Geng, Lihong; Chen, Zhijun; Zhang, Jian; Chen, Linjie; Liu, Donghao (August 2014). "Solar physics with Chinese Spectral Radioheliograph". 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS). Beijing, China: IEEE. pp. 1–4. doi:10.1109/URSIGASS.2014.6930043. ISBN 978-1-4673-5225-3. https://ieeexplore.ieee.org/document/6930043. 
  13. ↑ 13.0 13.1 Gary, Dale E.; Keller, Christoph U., eds (2005) (in en-gb). Solar and Space Weather Radiophysics. doi:10.1007/1-4020-2814-8. ISBN 978-1-4020-2813-7. https://link.springer.com/book/10.1007%2F1-4020-2814-8. 
  14. ↑ Zhang, PeiJin; Zucca, Pietro; Kozarev, Kamen; Carley, Eoin; Wang, ChuanBing; Franzen, Thomas; Dabrowski, Bartosz; Krankowski, Andrzej et al. (2022-06-01). "Imaging of the Quiet Sun in the Frequency Range of 20–80 MHz". The Astrophysical Journal 932 (1): 17. doi:10.3847/1538-4357/ac6b37. ISSN 0004-637X. Bibcode: 2022ApJ...932...17Z. 
  15. ↑ Aerts, Diederik (2009). Greenberger, Daniel. ed (in en). Compendium of Quantum Physics. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-540-70626-7. ISBN 978-3-540-70622-9. Bibcode: 2009cqp..book.....G. http://link.springer.com/10.1007/978-3-540-70626-7. 
  16. ↑ 16.00 16.01 16.02 16.03 16.04 16.05 16.06 16.07 16.08 16.09 16.10 16.11 Dulk, George A. (1985-09-01). "Radio Emission from the Sun and Stars". Annual Review of Astronomy and Astrophysics 23 (1): 169–224. doi:10.1146/annurev.aa.23.090185.001125. ISSN 0066-4146. Bibcode: 1985ARA&A..23..169D. https://www.annualreviews.org/doi/10.1146/annurev.aa.23.090185.001125. 
  17. ↑ 17.0 17.1 17.2 (in en) Physics of the Solar Corona. Springer Praxis Books. Springer Berlin Heidelberg. 2005. doi:10.1007/3-540-30766-4. ISBN 978-3-540-30765-5. http://link.springer.com/10.1007/3-540-30766-4. 
  18. ↑ 18.0 18.1 18.2 18.3 Melrose, D. B. (1986-08-14). Instabilities in Space and Laboratory Plasmas (1 ed.). Cambridge University Press. doi:10.1017/cbo9780511564123. ISBN 978-0-521-30541-9. https://www.cambridge.org/core/product/identifier/9780511564123/type/book. 
  19. ↑ Newkirk, Gordon Jr. (1961-05-01). "The Solar Corona in Active Regions and the Thermal Origin of the Slowly Varying Component of Solar Radio Radiation.". The Astrophysical Journal 133: 983. doi:10.1086/147104. ISSN 0004-637X. Bibcode: 1961ApJ...133..983N. 
  20. ↑ Bastian, T. S. (2007-08-10). "Synchrotron Radio Emission from a Fast Halo Coronal Mass Ejection" (in en). The Astrophysical Journal 665 (1): 805–812. doi:10.1086/519246. ISSN 0004-637X. Bibcode: 2007ApJ...665..805B. 
  21. ↑ White, S. M.; Kundu, M. R. (1997-08-01). "Radio Observations of Gyroresonance Emission from Coronal Magnetic Fields" (in en). Solar Physics 174 (1): 31–52. doi:10.1023/A:1004975528106. ISSN 1573-093X. Bibcode: 1997SoPh..174...31W. https://doi.org/10.1023/A:1004975528106. 
  22. ↑ Melrose, D. B. (1980-05-01). "The emission mechanisms for solar radio bursts" (in en). Space Science Reviews 26 (1): 3–38. doi:10.1007/BF00212597. ISSN 1572-9672. Bibcode: 1980SSRv...26....3M. https://doi.org/10.1007/BF00212597. 
  23. ↑ 23.0 23.1 23.2 23.3 23.4 Melrose, D. B. (September 2008). "Coherent emission" (in en). Proceedings of the International Astronomical Union 4 (S257): 305–315. doi:10.1017/S1743921309029470. ISSN 1743-9213. 
  24. ↑ Tonks, Lewi; Langmuir, Irving (1929-02-01). "Oscillations in Ionized Gases". Physical Review 33 (2): 195–210. doi:10.1103/PhysRev.33.195. PMID 16587379. Bibcode: 1929PhRv...33..195T. 
  25. ↑ Ginzburg, V. L.; Zhelezniakov, V. V. (1959). "On the mechanisms of sporadic solar radio emission". Symposium - International Astronomical Union 9: 574–582. doi:10.1017/s0074180900051494. ISSN 0074-1809. 
  26. ↑ Robinson, P. A.; Cairns, I. H. (2000), Stone, Robert G.; Weiler, Kurt W.; Goldstein, Melvyn L. et al., eds., "Theory of type III and type II solar radio emissions" (in en), Geophysical Monograph Series (Washington, D. C.: American Geophysical Union) 119: 37–45, doi:10.1029/gm119p0037, ISBN 978-0-87590-977-6, Bibcode: 2000GMS...119...37R, http://www.agu.org/books/gm/v119/GM119p0037/GM119p0037.shtml, retrieved 2021-01-18 
  27. ↑ Cairns, Iver H. (October 1987). "Fundamental plasma emission involving ion sound waves" (in en). Journal of Plasma Physics 38 (2): 169–178. doi:10.1017/S0022377800012496. ISSN 0022-3778. Bibcode: 1987JPlPh..38..169C. https://www.cambridge.org/core/product/identifier/S0022377800012496/type/journal_article. 
  28. ↑ Cairns, Iver H. (October 1987). "Second harmonic plasma emission involving ion sound waves" (in en). Journal of Plasma Physics 38 (2): 179–198. doi:10.1017/S0022377800012502. ISSN 1469-7807. Bibcode: 1987JPlPh..38..179C. https://www.cambridge.org/core/journals/journal-of-plasma-physics/article/abs/second-harmonic-plasma-emission-involving-ion-sound-waves/6121EABC5F0662A813F7556CEA7D77E9. 
  29. ↑ 29.0 29.1 29.2 McCauley, Patrick I.; Cairns, Iver H.; White, Stephen M.; Mondal, Surajit; Lenc, Emil; Morgan, John; Oberoi, Divya (August 2019). "The Low-Frequency Solar Corona in Circular Polarization" (in en). Solar Physics 294 (8): 106. doi:10.1007/s11207-019-1502-y. ISSN 0038-0938. Bibcode: 2019SoPh..294..106M. http://link.springer.com/10.1007/s11207-019-1502-y. 
  30. ↑ 30.0 30.1 McCauley, Patrick I.; Cairns, Iver H.; Morgan, John (2018-10-01). "Densities Probed by Coronal Type III Radio Burst Imaging" (in en). Solar Physics 293 (10): 132. doi:10.1007/s11207-018-1353-y. ISSN 1573-093X. Bibcode: 2018SoPh..293..132M. https://doi.org/10.1007/s11207-018-1353-y. 
  31. ↑ Reid, Mark J.; Moran, James M. (September 1981). "Masers" (in en). Annual Review of Astronomy and Astrophysics 19 (1): 231–276. doi:10.1146/annurev.aa.19.090181.001311. ISSN 0066-4146. Bibcode: 1981ARA&A..19..231R. http://www.annualreviews.org/doi/10.1146/annurev.aa.19.090181.001311. 
  32. ↑ 32.0 32.1 Treumann, Rudolf A. (2006-08-01). "The electron–cyclotron maser for astrophysical application" (in en). The Astronomy and Astrophysics Review 13 (4): 229–315. doi:10.1007/s00159-006-0001-y. ISSN 1432-0754. Bibcode: 2006A&ARv..13..229T. https://doi.org/10.1007/s00159-006-0001-y. 
  33. ↑ Wu, C. S.; Lee, L. C. (June 1979). "A theory of the terrestrial kilometric radiation" (in en). The Astrophysical Journal 230: 621. doi:10.1086/157120. ISSN 0004-637X. Bibcode: 1979ApJ...230..621W. http://adsabs.harvard.edu/doi/10.1086/157120. 
  34. ↑ Holman, G. D.; Eichler, D.; Kundu, M. R. (1980), Kundu, Mukul R.; Gergely, Tomas E., eds., "An Interpretation of Solar Flare Microwave Spikes as Gyrosynchrotron Masering" (in en), Radio Physics of the Sun (Dordrecht: Springer Netherlands): pp. 457–459, doi:10.1007/978-94-010-9722-2_65, ISBN 978-90-277-1121-2, http://link.springer.com/10.1007/978-94-010-9722-2_65, retrieved 2023-08-15 
  35. ↑ Winglee, R. M.; Dulk, G. A. (November 1986). "The electron-cyclotron maser instability as the source of solar type V continuum" (in en). The Astrophysical Journal 310: 432. doi:10.1086/164696. ISSN 0004-637X. Bibcode: 1986ApJ...310..432W. http://adsabs.harvard.edu/doi/10.1086/164696. 
  36. ↑ Aschwanden, M. J.; Benz, A. O. (1988-09-01). "On the Electron-Cyclotron Maser Instability. II. Pulsations in the Quasi-stationary State". The Astrophysical Journal 332: 466. doi:10.1086/166670. ISSN 0004-637X. Bibcode: 1988ApJ...332..466A. http://adsabs.harvard.edu/abs/1988ApJ...332..466A. 
  37. ↑ Ginzburg, V. L. (Vitaliĭ Lazarevich), 1916-2009. (1970). The propagation of electromagnetic waves in plasmas (2d ed., rev. and enl ed.). Oxford: Pergamon Press. ISBN 0-08-015569-3. OCLC 153074. https://www.worldcat.org/oclc/153074. 
  38. ↑ Koskinen, Hannu E. J. (Hannu Erkki Juhani), 1954- (2011). Physics of space storms : from the solar surface the Earth. Berlin: Springer. ISBN 978-3-642-00319-6. OCLC 704396917. https://www.worldcat.org/oclc/704396917. 
  39. ↑ Alissandrakis, C. E.; Chiuderi-Drago, F. (June 1994). "Detection of linear polarization in the microwave emission of Solar Active Regions" (in en). The Astrophysical Journal 428: L73. doi:10.1086/187396. ISSN 0004-637X. Bibcode: 1994ApJ...428L..73A. 
  40. ↑ Schrijver, Carolus J., ed (2010). Heliophysics: Space Storms and Radiation: Causes and Effects. Cambridge: Cambridge University Press. doi:10.1017/cbo9781139194532. ISBN 978-0-521-76051-5. https://www.cambridge.org/core/books/heliophysics-space-storms-and-radiation-causes-and-effects/608857F4EEE1C0BF61F26ACD19BA59DE. 
  41. ↑ Spangler, Steven R. (2007-11-20). "A Technique for Measuring Electrical Currents in the Solar Corona" (in en). The Astrophysical Journal 670 (1): 841–848. doi:10.1086/521995. ISSN 0004-637X. Bibcode: 2007ApJ...670..841S. https://iopscience.iop.org/article/10.1086/521995. 
  42. ↑ Ingleby, Laura D.; Spangler, Steven R.; Whiting, Catherine A. (2007-10-10). "Probing the Large‐Scale Plasma Structure of the Solar Corona with Faraday Rotation Measurements" (in en). The Astrophysical Journal 668 (1): 520–532. doi:10.1086/521140. ISSN 0004-637X. Bibcode: 2007ApJ...668..520I. https://iopscience.iop.org/article/10.1086/521140. 
  43. ↑ Sharma, Rohit; Oberoi, Divya (2020-11-10). "Propagation Effects in Quiet Sun Observations at Meter Wavelengths". The Astrophysical Journal 903 (2): 126. doi:10.3847/1538-4357/abb949. ISSN 1538-4357. Bibcode: 2020ApJ...903..126S. 
  44. ↑ Stewart, R. T. (1976-11-01). "Source heights of metre wavelength bursts of spectral types I and III" (in en). Solar Physics 50 (2): 437–445. doi:10.1007/BF00155305. ISSN 1573-093X. Bibcode: 1976SoPh...50..437S. https://doi.org/10.1007/BF00155305. 
  45. ↑ Mann, G.; Breitling, F.; Vocks, C.; Aurass, H.; Steinmetz, M.; Strassmeier, K. G.; Bisi, M. M.; Fallows, R. A. et al. (2018-03-01). "Tracking of an electron beam through the solar corona with LOFAR" (in en). Astronomy & Astrophysics 611: A57. doi:10.1051/0004-6361/201629017. ISSN 0004-6361. Bibcode: 2018A&A...611A..57M. https://www.aanda.org/articles/aa/abs/2018/03/aa29017-16/aa29017-16.html. 
  46. ↑ Stewart, R. T.; McLean, D. J. (1982). "Correcting Low-Frequency Solar Radio Source Positions for Ionospheric Refraction" (in en). Publications of the Astronomical Society of Australia 4 (4): 386–389. doi:10.1017/S1323358000021226. ISSN 1323-3580. Bibcode: 1982PASA....4..386S. https://www.cambridge.org/core/journals/publications-of-the-astronomical-society-of-australia/article/abs/correcting-lowfrequency-solar-radio-source-positions-for-ionospheric-refraction/A1767245E939A7EF19AA6156D43EA2DE. 
  47. ↑ Dulk, George A. (2000), "Type III solar radio bursts at long wavelengths", in Stone, Robert G.; Weiler, Kurt W.; Goldstein, Melvyn L. et al. (in en), Radio Astronomy at Long Wavelengths, Geophysical Monograph Series, 119, Washington, D. C.: American Geophysical Union, pp. 115–122, doi:10.1029/gm119p0115, ISBN 978-0-87590-977-6, http://www.agu.org/books/gm/v119/GM119p0115/GM119p0115.shtml, retrieved 2021-01-18 
  48. ↑ Bastian, T. S. (May 1994). "Angular scattering of solar radio emission by coronal turbulence" (in en). The Astrophysical Journal 426: 774. doi:10.1086/174114. ISSN 0004-637X. Bibcode: 1994ApJ...426..774B. 
  49. ↑ Ingale, M.; Subramanian, P.; Cairns, Iver (2015-03-11). "Coronal turbulence and the angular broadening of radio sources – the role of the structure function" (in en). Monthly Notices of the Royal Astronomical Society 447 (4): 3486–3497. doi:10.1093/mnras/stu2703. ISSN 1365-2966. http://academic.oup.com/mnras/article/447/4/3486/1750614/Coronal-turbulence-and-the-angular-broadening-of. 
  50. ↑ Dulk, G. A.; Steinberg, J. L.; Lecacheux, A.; Hoang, S.; MacDowall, R. J. (1985). "The visibility of type III radio bursts originating behind the sun". Astronomy and Astrophysics 150 (2): L28–L30. Bibcode: 1985A&A...150L..28D. https://ui.adsabs.harvard.edu/abs/1985A%26A...150L..28D/abstract. 
  51. ↑ Robinson, R. D. (1983). "Scattering of Radio Waves in the Solar Corona" (in en). Publications of the Astronomical Society of Australia 5 (2): 208–211. doi:10.1017/S132335800001688X. ISSN 1323-3580. Bibcode: 1983PASA....5..208R. https://www.cambridge.org/core/product/identifier/S132335800001688X/type/journal_article. 
  52. ↑ 52.0 52.1 Melrose, D. B. (February 2006). "Depolarization of Radio Bursts Due to Reflection off Sharp Boundaries in the Solar Corona" (in en). The Astrophysical Journal 637 (2): 1113–1121. doi:10.1086/498499. ISSN 0004-637X. Bibcode: 2006ApJ...637.1113M. https://iopscience.iop.org/article/10.1086/498499. 
  53. ↑ (in en) Radio Emission of the Sun and Planets. Elsevier. 1970. doi:10.1016/c2013-0-02176-7. ISBN 978-0-08-013061-3. https://linkinghub.elsevier.com/retrieve/pii/C20130021767. 
  54. ↑ Gary, Dale E., ed (2005) (in en). Solar and Space Weather Radiophysics: Current Status and Future Developments. Dordrecht: Springer Netherlands. doi:10.1007/1-4020-2814-8. ISBN 978-1-4020-2813-7. http://link.springer.com/10.1007/1-4020-2814-8. 
  55. ↑ Cohen, M. H. (May 1960). "Magnetoionic Mode Coupling at High Frequencies." (in en). The Astrophysical Journal 131: 664. doi:10.1086/146878. ISSN 0004-637X. Bibcode: 1960ApJ...131..664C. 
  56. ↑ Brosius, J. W.; Holman, G. D.; Schmelz, J. T. (1991). "Microwave polarization inversion observed" (in en). Eos, Transactions American Geophysical Union 72 (42): 449. doi:10.1029/90EO00328. ISSN 0096-3941. http://doi.wiley.com/10.1029/90EO00328. 
  57. ↑ Ryabov, B.I.; Pilyeva, N.A.; Alissandrakis, C.E.; Shibasaki, K.; Bogod, V.M.; Garaimov, V.I.; Gelfreikh, G.B. (1999). "Coronal Magnetography of an Active Region From Microwave Polarization Inversion". Solar Physics 185 (1): 157–175. doi:10.1023/A:1005114303703. Bibcode: 1999SoPh..185..157R. http://link.springer.com/10.1023/A:1005114303703. 
  58. ↑ White, S. M.; Thejappa, G.; Kundu, M. R. (March 1992). "Observations of mode coupling in the solar corona and bipolar noise storms" (in en). Solar Physics 138 (1): 163–187. doi:10.1007/BF00146202. ISSN 0038-0938. Bibcode: 1992SoPh..138..163W. http://link.springer.com/10.1007/BF00146202. 
  59. ↑ ELGAROY, E.O. (1977), "Metric Noise Storms and Related Phenomena", Solar Noise Storms (Elsevier): pp. 186–209, doi:10.1016/b978-0-08-021039-1.50014-7, ISBN 978-0-08-021039-1, http://dx.doi.org/10.1016/b978-0-08-021039-1.50014-7, retrieved 2021-01-18 
  60. ↑ Second Advances in Solar Physic[s Euroconference : three-dimensional structure of solar active regions : proceedings of a meeting held in Preveza, Greece, 7-11 October 1997]. Alissandrakis, C. E. (Constantine E.), 1948-, Schmieder, Brigitte.. San Francisco, Calif.: Astronomical Society of the Pacific. 1998. ISBN 1-886733-75-9. OCLC 40864809. https://www.worldcat.org/oclc/40864809. 
  61. ↑ Gergely, Tomas E.; Erickson, William C. (June 1975). "Decameter storm radiation, I" (in en). Solar Physics 42 (2): 467–486. doi:10.1007/BF00149927. ISSN 0038-0938. Bibcode: 1975SoPh...42..467G. http://link.springer.com/10.1007/BF00149927. 
  62. ↑ Priest, Eric (2013), "The Basic Equations of Magnetohydrodynamics (MHD)", Magnetohydrodynamics of the Sun (Cambridge: Cambridge University Press): pp. 74–106, doi:10.1017/cbo9781139020732.003, ISBN 978-1-139-02073-2, http://dx.doi.org/10.1017/cbo9781139020732.003, retrieved 2021-01-18 
  63. ↑ Willson, Robert F. (April 2005). "Very Large Array and SOHO Observations of Type I Noise Storms, Large-Scale Loops and Magnetic Restructuring in the Corona" (in en). Solar Physics 227 (2): 311–326. doi:10.1007/s11207-005-1104-8. ISSN 0038-0938. Bibcode: 2005SoPh..227..311W. http://link.springer.com/10.1007/s11207-005-1104-8. 
  64. ↑ Li, C. Y.; Chen, Y.; Wang, B.; Ruan, G. P.; Feng, S. W.; Du, G. H.; Kong, X. L. (June 2017). "EUV and Magnetic Activities Associated with Type-I Solar Radio Bursts" (in en). Solar Physics 292 (6): 82. doi:10.1007/s11207-017-1108-1. ISSN 0038-0938. Bibcode: 2017SoPh..292...82L. http://link.springer.com/10.1007/s11207-017-1108-1. 
  65. ↑ Benz, A. O.; Wentzel, D. G. (1980), "Solar Type I Radio Bursts: An Ion-Acoustic Wave Model", Radio Physics of the Sun (Dordrecht: Springer Netherlands): pp. 251–254, doi:10.1007/978-94-010-9722-2_34, ISBN 978-90-277-1121-2, http://dx.doi.org/10.1007/978-94-010-9722-2_34, retrieved 2021-01-18 
  66. ↑ Spicer, D. S.; Benz, A. O.; Huba, J. D. (1982). "Solar type I noise storms and newly emerging magnetic flux". Astron. Astrophys. 105 (2): 221–228. Bibcode: 1982A&A...105..221S. https://ui.adsabs.harvard.edu/abs/1982A%26A...105..221S/abstract. 
  67. ↑ Del Zanna, G.; Aulanier, G.; Klein, K.-L.; Török, T. (2011-01-12). "A single picture for solar coronal outflows and radio noise storms". Astronomy & Astrophysics 526: A137. doi:10.1051/0004-6361/201015231. ISSN 0004-6361. Bibcode: 2011A&A...526A.137D. 
  68. ↑ Bentley, R.D.; Klein, K.-L.; van Driel-Gesztelyi, L.; Démoulin, P.; Trottet, G.; Tassetto, P.; Marty, G. (2000). "Magnetic Activity Associated With Radio Noise Storms". Solar Physics 193 (1/2): 227–245. doi:10.1023/A:1005218007132. Bibcode: 2000SoPh..193..227B. http://link.springer.com/10.1023/A:1005218007132. 
  69. ↑ Kumari, Anshu (30 May 2023). "Type II radio bursts and their association with coronal mass ejections in solar cycles 23 and 24". arXiv preprint arXiv:2305.18992. doi:10.1051/0004-6361/202244015. 
  70. ↑ Roberts, Ja (1959). "Solar Radio Bursts of Spectral Type II" (in en). Australian Journal of Physics 12 (4): 327. doi:10.1071/PH590327. ISSN 0004-9506. Bibcode: 1959AuJPh..12..327R. http://www.publish.csiro.au/?paper=PH590327. 
  71. ↑ Sturrock, P. A. (October 1961). "Spectral Characteristics of Type II Solar Radio Bursts" (in en). Nature 192 (4797): 58. doi:10.1038/192058a0. ISSN 0028-0836. Bibcode: 1961Natur.192...58S. 
  72. ↑ Cane, H. V.; Stone, R. G. (July 1984). "Type II solar radio bursts, interplanetary shocks, and energetic particle events" (in en). The Astrophysical Journal 282: 339. doi:10.1086/162207. ISSN 0004-637X. Bibcode: 1984ApJ...282..339C. 
  73. ↑ Miralles, Mari Paz, ed (2011) (in en). The Sun, the Solar Wind, and the Heliosphere. Dordrecht: Springer Netherlands. doi:10.1007/978-90-481-9787-3. ISBN 978-90-481-9786-6. http://link.springer.com/10.1007/978-90-481-9787-3. 
  74. ↑ Komesaroff, M. (1958). "Polarization Measurements of the Three Spectral Types of Solar Radio Burst" (in en). Australian Journal of Physics 11 (2): 201–214. doi:10.1071/ph580201. ISSN 1446-5582. Bibcode: 1958AuJPh..11..201K. https://www.publish.csiro.au/ph/ph580201. 
  75. ↑ 75.0 75.1 75.2 75.3 McLean, D. J., and N. R. Labrum (1985). Solar radiophysics: Studies of emission from the sun at metre wavelengths. Cambridge University Press. Bibcode: 1985srph.book.....M. https://ui.adsabs.harvard.edu/abs/1985srph.book.....M/abstract. 
  76. ↑ 76.0 76.1 Cairns, I. H.; Robinson, R. D. (1987). "Herringbone bursts associated with type II solar radio emission" (in en). Solar Physics 111 (2): 365–383. doi:10.1007/BF00148526. ISSN 0038-0938. Bibcode: 1987SoPh..111..365C. http://link.springer.com/10.1007/BF00148526. 
  77. ↑ Mann, G.; Melnik, V. N.; Rucker, H. O.; Konovalenko, A. A.; Brazhenko, A. I. (2018). "Radio signatures of shock-accelerated electron beams in the solar corona". Astronomy & Astrophysics 609: A41. doi:10.1051/0004-6361/201730546. ISSN 0004-6361. https://www.aanda.org/10.1051/0004-6361/201730546. 
  78. ↑ 78.0 78.1 78.2 78.3 Reid, Hamish Andrew Sinclair; Ratcliffe, Heather (July 2014). "A review of solar type III radio bursts". Research in Astronomy and Astrophysics 14 (7): 773–804. doi:10.1088/1674-4527/14/7/003. ISSN 1674-4527. Bibcode: 2014RAA....14..773R. https://iopscience.iop.org/article/10.1088/1674-4527/14/7/003. 
  79. ↑ Robinson, P. A.; Cairns, I. H. (2000), Stone, Robert G.; Weiler, Kurt W.; Goldstein, Melvyn L. et al., eds., "Theory of type III and type II solar radio emissions" (in en), Geophysical Monograph Series (Washington, D. C.: American Geophysical Union) 119: 37–45, doi:10.1029/gm119p0037, ISBN 978-0-87590-977-6, Bibcode: 2000GMS...119...37R, http://www.agu.org/books/gm/v119/GM119p0037/GM119p0037.shtml, retrieved 2021-01-23 
  80. ↑ Benz, Arnold O.; Grigis, Paolo C.; Csillaghy, AndrÉ; Saint-Hilaire, Pascal (January 2005). "Survey on Solar X-ray Flares and Associated Coherent Radio Emissions" (in en). Solar Physics 226 (1): 121–142. doi:10.1007/s11207-005-5254-5. ISSN 0038-0938. Bibcode: 2005SoPh..226..121B. http://link.springer.com/10.1007/s11207-005-5254-5. 
  81. ↑ Benz, Arnold O.; Brajša, Roman; Magdalenić, Jasmina (February 2007). "Are There Radio-quiet Solar Flares?" (in en). Solar Physics 240 (2): 263–270. doi:10.1007/s11207-007-0365-9. ISSN 0038-0938. Bibcode: 2007SoPh..240..263B. http://link.springer.com/10.1007/s11207-007-0365-9. 
  82. ↑ Reid, Hamish A. S.; Vilmer, Nicole (January 2017). "Coronal type III radio bursts and their X-ray flare and interplanetary type III counterparts". Astronomy & Astrophysics 597: A77. doi:10.1051/0004-6361/201527758. ISSN 0004-6361. Bibcode: 2017A&A...597A..77R. 
  83. ↑ McCauley, Patrick I.; Cairns, Iver H.; Morgan, John; Gibson, Sarah E.; Harding, James C.; Lonsdale, Colin; Oberoi, Divya (2017-12-22). "Type III Solar Radio Burst Source Region Splitting due to a Quasi-separatrix Layer". The Astrophysical Journal 851 (2): 151. doi:10.3847/1538-4357/aa9cee. ISSN 1538-4357. Bibcode: 2017ApJ...851..151M. 
  84. ↑ Frank, L. A.; Gurnett, D. A. (December 1972). "Direct observations of low-energy solar electrons associated with a type III solar radio burst". Solar Physics 27 (2): 446–465. doi:10.1007/bf00153116. ISSN 0038-0938. Bibcode: 1972SoPh...27..446F. http://dx.doi.org/10.1007/bf00153116. 
  85. ↑ Gurnett, D. A.; Anderson, R. R. (1976-12-10). "Electron Plasma Oscillations Associated with Type III Radio Bursts" (in en). Science 194 (4270): 1159–1162. doi:10.1126/science.194.4270.1159. ISSN 0036-8075. PMID 17790910. Bibcode: 1976Sci...194.1159G. https://www.science.org/doi/10.1126/science.194.4270.1159. 
  86. ↑ Wentzel, Donat G. (January 1984). "Polarization of fundamental type III radio bursts" (in en). Solar Physics 90 (1): 139–159. doi:10.1007/BF00153791. ISSN 0038-0938. Bibcode: 1984SoPh...90..139W. http://link.springer.com/10.1007/BF00153791. 
  87. ↑ Boischot, A.; Warwick, J. W. (June 1959). "Radio emission following the flare of August 22, 1958". Journal of Geophysical Research 64 (6): 683–684. doi:10.1029/jz064i006p00683. ISSN 0148-0227. Bibcode: 1959JGR....64..683B. http://dx.doi.org/10.1029/jz064i006p00683. 
  88. ↑ Morosan, D. E.; Kilpua, E. K. J.; Carley, E. P.; Monstein, C. (March 2019). "Variable emission mechanism of a Type IV radio burst". Astronomy & Astrophysics 623: A63. doi:10.1051/0004-6361/201834510. ISSN 0004-6361. Bibcode: 2019A&A...623A..63M. 
  89. ↑ Pick-Gutmann, M. (1961). "Évolution des émissions radioélectriques solaires de type IV et leur relation avec d'autres phénomènes solaires et géophysiques". Annales d'Astrophysique 24: 183. Bibcode: 1961AnAp...24..183P. https://ui.adsabs.harvard.edu/abs/1961AnAp...24..183P/abstract. 
  90. ↑ Zheleznyakov, V. V., and V. V. Zaitsev (1968). "The Origin of Type-V Solar Radio Bursts". Soviet Astron. 12: 14. Bibcode: 1968SvA....12...14Z. https://ui.adsabs.harvard.edu/abs/1968SvA....12...14Z/abstract. 
  91. ↑ Robinson, R. D. (December 1977). "A study of Type V solar radio bursts: I: Observations" (in en). Solar Physics 55 (2): 459–472. doi:10.1007/BF00152587. ISSN 0038-0938. Bibcode: 1977SoPh...55..459R. http://link.springer.com/10.1007/BF00152587. 
  92. ↑ Dulk, G. A., D. E. Gary, and S. Suzuki (1980). "The position and polarization of Type V solar bursts". Astronomy and Astrophysics 88 (1–2): 218–229. Bibcode: 1980A&A....88..218D. https://ui.adsabs.harvard.edu/abs/1980A%26A....88..218D/abstract. 
  93. ↑ Tang, J. F.; Wu, D. J.; Tan, C. M. (2013-11-26). "Electron Cyclotron Maser Emission in Coronal Arches and Solar Radio Type V Bursts". The Astrophysical Journal 779 (1): 83. doi:10.1088/0004-637X/779/1/83. ISSN 0004-637X. Bibcode: 2013ApJ...779...83T. 
  94. ↑ Slottje, C. (July 1972). "Peculiar absorption and emission microstructures in the type IV solar radio outburst of March 2, 1970" (in en). Solar Physics 25 (1): 210–231. doi:10.1007/BF00155758. ISSN 0038-0938. Bibcode: 1972SoPh...25..210S. http://link.springer.com/10.1007/BF00155758. 
  95. ↑ Aurass, H.; Rausche, G.; Mann, G.; Hofmann, A. (2005-05-13). "Fiber bursts as 3D coronal magnetic field probe in postflare loops". Astronomy & Astrophysics 435 (3): 1137–1148. doi:10.1051/0004-6361:20042199. ISSN 0004-6361. Bibcode: 2005A&A...435.1137A. 
  96. ↑ Reid, Hamish A. S. (August 2016). "Solar type III bursts observed with LOFAR". 2016 URSI Asia-Pacific Radio Science Conference (URSI AP-RASC). IEEE. pp. 1235–1238. doi:10.1109/ursiap-rasc.2016.7601384. ISBN 978-1-4673-8801-6. http://dx.doi.org/10.1109/ursiap-rasc.2016.7601384. 
  97. ↑ Kundu, MukulR.; Vlahos, Loukas (1982). "Solar microwave bursts ? A review" (in en). Space Science Reviews 32 (4): 405. doi:10.1007/BF00177449. ISSN 0038-6308. Bibcode: 1982SSRv...32..405K. http://link.springer.com/10.1007/BF00177449. 
  98. ↑ Johnston, K. J.; Fey, A. L.; Gaume, R. A.; Claussen, M. J.; Hummel, C. A. (August 2004). "Recent Observations of the Centimeter Radio Emission from the T Tauri System". The Astronomical Journal 128 (2): 822–828. doi:10.1086/422490. ISSN 0004-6256. Bibcode: 2004AJ....128..822J. 
  99. ↑ 99.0 99.1 Melrose, D B; Rafat, M Z (December 2017). "Pulsar radio emission mechanism: Why no consensus?". Journal of Physics: Conference Series 932 (1): 012011. doi:10.1088/1742-6596/932/1/012011. ISSN 1742-6588. Bibcode: 2017JPhCS.932a2011M. 
  100. ↑ Melrose, D. B. (June 1995). "The models for radio emission from pulsars–The outstanding issues". Journal of Astrophysics and Astronomy 16 (2): 137–164. doi:10.1007/bf02714830. ISSN 0250-6335. Bibcode: 1995JApA...16..137M. http://dx.doi.org/10.1007/bf02714830. 

Further reading



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Solar_radio_emission&oldid=3343941"