Statistical significance
In statistical hypothesis testing,[1][2] a result has statistical significance when a result at least as "extreme" would be very infrequent if the null hypothesis were true.[3] More precisely, a study's defined significance level, denoted by [math]\displaystyle{ \alpha }[/math], is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true;[4] and the p-value of a result, [math]\displaystyle{ p }[/math], is the probability of obtaining a result at least as extreme, given that the null hypothesis is true.[5] The result is statistically significant, by the standards of the study, when [math]\displaystyle{ p \le \alpha }[/math].[6][7][8][9][10][11][12] The significance level for a study is chosen before data collection, and is typically set to 5%[13] or much lower—depending on the field of study.[14]
In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone.[15][16] But if the p-value of an observed effect is less than (or equal to) the significance level, an investigator may conclude that the effect reflects the characteristics of the whole population,[1] thereby rejecting the null hypothesis.[17]
This technique for testing the statistical significance of results was developed in the early 20th century. The term significance does not imply importance here, and the term statistical significance is not the same as research significance, theoretical significance, or practical significance.[1][2][18][19] For example, the term clinical significance refers to the practical importance of a treatment effect.[20]
History
Statistical significance dates to the 18th century, in the work of John Arbuthnot and Pierre-Simon Laplace, who computed the p-value for the human sex ratio at birth, assuming a null hypothesis of equal probability of male and female births; see p-value § History for details.[21][22][23][24][25][26][27]
In 1925, Ronald Fisher advanced the idea of statistical hypothesis testing, which he called "tests of significance", in his publication Statistical Methods for Research Workers.[28][29][30] Fisher suggested a probability of one in twenty (0.05) as a convenient cutoff level to reject the null hypothesis.[31] In a 1933 paper, Jerzy Neyman and Egon Pearson called this cutoff the significance level, which they named [math]\displaystyle{ \alpha }[/math]. They recommended that [math]\displaystyle{ \alpha }[/math] be set ahead of time, prior to any data collection.[31][32]
Despite his initial suggestion of 0.05 as a significance level, Fisher did not intend this cutoff value to be fixed. In his 1956 publication Statistical Methods and Scientific Inference, he recommended that significance levels be set according to specific circumstances.[31]
Related concepts
The significance level [math]\displaystyle{ \alpha }[/math] is the threshold for [math]\displaystyle{ p }[/math] below which the null hypothesis is rejected even though by assumption it were true, and something else is going on. This means that [math]\displaystyle{ \alpha }[/math] is also the probability of mistakenly rejecting the null hypothesis, if the null hypothesis is true.[4] This is also called false positive and type I error.
Sometimes researchers talk about the confidence level γ = (1 − α) instead. This is the probability of not rejecting the null hypothesis given that it is true.[33][34] Confidence levels and confidence intervals were introduced by Neyman in 1937.[35]
Role in statistical hypothesis testing
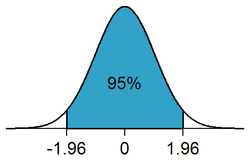
Statistical significance plays a pivotal role in statistical hypothesis testing. It is used to determine whether the null hypothesis should be rejected or retained. The null hypothesis is the hypothesis that no effect exists in the phenomenon being studied.[36] For the null hypothesis to be rejected, an observed result has to be statistically significant, i.e. the observed p-value is less than the pre-specified significance level [math]\displaystyle{ \alpha }[/math].
To determine whether a result is statistically significant, a researcher calculates a p-value, which is the probability of observing an effect of the same magnitude or more extreme given that the null hypothesis is true.[5][12] The null hypothesis is rejected if the p-value is less than (or equal to) a predetermined level, [math]\displaystyle{ \alpha }[/math]. [math]\displaystyle{ \alpha }[/math] is also called the significance level, and is the probability of rejecting the null hypothesis given that it is true (a type I error). It is usually set at or below 5%.
For example, when [math]\displaystyle{ \alpha }[/math] is set to 5%, the conditional probability of a type I error, given that the null hypothesis is true, is 5%,[37] and a statistically significant result is one where the observed p-value is less than (or equal to) 5%.[38] When drawing data from a sample, this means that the rejection region comprises 5% of the sampling distribution.[39] These 5% can be allocated to one side of the sampling distribution, as in a one-tailed test, or partitioned to both sides of the distribution, as in a two-tailed test, with each tail (or rejection region) containing 2.5% of the distribution.
The use of a one-tailed test is dependent on whether the research question or alternative hypothesis specifies a direction such as whether a group of objects is heavier or the performance of students on an assessment is better.[3] A two-tailed test may still be used but it will be less powerful than a one-tailed test, because the rejection region for a one-tailed test is concentrated on one end of the null distribution and is twice the size (5% vs. 2.5%) of each rejection region for a two-tailed test. As a result, the null hypothesis can be rejected with a less extreme result if a one-tailed test was used.[40] The one-tailed test is only more powerful than a two-tailed test if the specified direction of the alternative hypothesis is correct. If it is wrong, however, then the one-tailed test has no power.
Significance thresholds in specific fields
In specific fields such as particle physics and manufacturing, statistical significance is often expressed in multiples of the standard deviation or sigma (σ) of a normal distribution, with significance thresholds set at a much stricter level (for example 5σ).[41][42] For instance, the certainty of the Higgs boson particle's existence was based on the 5σ criterion, which corresponds to a p-value of about 1 in 3.5 million.[42][43]
In other fields of scientific research such as genome-wide association studies, significance levels as low as 5×10−8 are not uncommon[44][45]—as the number of tests performed is extremely large.
Limitations
Researchers focusing solely on whether their results are statistically significant might report findings that are not substantive[46] and not replicable.[47][48] There is also a difference between statistical significance and practical significance. A study that is found to be statistically significant may not necessarily be practically significant.[49][19]
Effect size
Effect size is a measure of a study's practical significance.[49] A statistically significant result may have a weak effect. To gauge the research significance of their result, researchers are encouraged to always report an effect size along with p-values. An effect size measure quantifies the strength of an effect, such as the distance between two means in units of standard deviation (cf. Cohen's d), the correlation coefficient between two variables or its square, and other measures.[50]
Reproducibility
A statistically significant result may not be easy to reproduce.[48] In particular, some statistically significant results will in fact be false positives. Each failed attempt to reproduce a result increases the likelihood that the result was a false positive.[51]
Challenges
Overuse in some journals
Starting in the 2010s, some journals began questioning whether significance testing, and particularly using a threshold of α=5%, was being relied on too heavily as the primary measure of validity of a hypothesis.[52] Some journals encouraged authors to do more detailed analysis than just a statistical significance test. In social psychology, the journal Basic and Applied Social Psychology banned the use of significance testing altogether from papers it published,[53] requiring authors to use other measures to evaluate hypotheses and impact.[54][55]
Other editors, commenting on this ban have noted: "Banning the reporting of p-values, as Basic and Applied Social Psychology recently did, is not going to solve the problem because it is merely treating a symptom of the problem. There is nothing wrong with hypothesis testing and p-values per se as long as authors, reviewers, and action editors use them correctly."[56] Some statisticians prefer to use alternative measures of evidence, such as likelihood ratios or Bayes factors.[57] Using Bayesian statistics can avoid confidence levels, but also requires making additional assumptions,[57] and may not necessarily improve practice regarding statistical testing.[58]
The widespread abuse of statistical significance represents an important topic of research in metascience.[59]
Redefining significance
In 2016, the American Statistical Association (ASA) published a statement on p-values, saying that "the widespread use of 'statistical significance' (generally interpreted as 'p ≤ 0.05') as a license for making a claim of a scientific finding (or implied truth) leads to considerable distortion of the scientific process".[57] In 2017, a group of 72 authors proposed to enhance reproducibility by changing the p-value threshold for statistical significance from 0.05 to 0.005.[60] Other researchers responded that imposing a more stringent significance threshold would aggravate problems such as data dredging; alternative propositions are thus to select and justify flexible p-value thresholds before collecting data,[61] or to interpret p-values as continuous indices, thereby discarding thresholds and statistical significance.[62] Additionally, the change to 0.005 would increase the likelihood of false negatives, whereby the effect being studied is real, but the test fails to show it.[63]
In 2019, over 800 statisticians and scientists signed a message calling for the abandonment of the term "statistical significance" in science,[64] and the ASA published a further official statement [65] declaring (page 2):
We conclude, based on our review of the articles in this special issue and the broader literature, that it is time to stop using the term "statistically significant" entirely. Nor should variants such as "significantly different," "[math]\displaystyle{ p \le 0.05 }[/math]," and "nonsignificant" survive, whether expressed in words, by asterisks in a table, or in some other way.
See also
- A/B testing, ABX test
- Estimation statistics
- Fisher's method for combining independent tests of significance
- Look-elsewhere effect
- Multiple comparisons problem
- Sample size
- Texas sharpshooter fallacy (gives examples of tests where the significance level was set too high)
References
- ↑ 1.0 1.1 1.2 Sirkin, R. Mark (2005). "Two-sample t tests". Statistics for the Social Sciences (3rd ed.). Thousand Oaks, CA: SAGE Publications, Inc. pp. 271–316. ISBN 978-1-412-90546-6.
- ↑ 2.0 2.1 Borror, Connie M. (2009). "Statistical decision making". The Certified Quality Engineer Handbook (3rd ed.). Milwaukee, WI: ASQ Quality Press. pp. 418–472. ISBN 978-0-873-89745-7.
- ↑ 3.0 3.1 Myers, Jerome L.; Well, Arnold D.; Lorch, Robert F. Jr. (2010). "Developing fundamentals of hypothesis testing using the binomial distribution". Research design and statistical analysis (3rd ed.). New York, NY: Routledge. pp. 65–90. ISBN 978-0-805-86431-1.
- ↑ 4.0 4.1 Dalgaard, Peter (2008). "Power and the computation of sample size". Introductory Statistics with R. Statistics and Computing. New York: Springer. pp. 155–56. doi:10.1007/978-0-387-79054-1_9. ISBN 978-0-387-79053-4.
- ↑ 5.0 5.1 "Statistical Hypothesis Testing". http://www.dartmouth.edu/~matc/X10/Show.htm.
- ↑ Johnson, Valen E. (October 9, 2013). "Revised standards for statistical evidence". Proceedings of the National Academy of Sciences 110 (48): 19313–19317. doi:10.1073/pnas.1313476110. PMID 24218581. Bibcode: 2013PNAS..11019313J.
- ↑ Redmond, Carol; Colton, Theodore (2001). "Clinical significance versus statistical significance". Biostatistics in Clinical Trials. Wiley Reference Series in Biostatistics (3rd ed.). West Sussex, United Kingdom: John Wiley & Sons Ltd. pp. 35–36. ISBN 978-0-471-82211-0.
- ↑ Cumming, Geoff (2012). Understanding The New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York, USA: Routledge. pp. 27–28.
- ↑ Krzywinski, Martin; Altman, Naomi (30 October 2013). "Points of significance: Significance, P values and t-tests". Nature Methods 10 (11): 1041–1042. doi:10.1038/nmeth.2698. PMID 24344377.
- ↑ Sham, Pak C.; Purcell, Shaun M (17 April 2014). "Statistical power and significance testing in large-scale genetic studies". Nature Reviews Genetics 15 (5): 335–346. doi:10.1038/nrg3706. PMID 24739678.
- ↑ Altman, Douglas G. (1999). Practical Statistics for Medical Research. New York, USA: Chapman & Hall/CRC. pp. 167. ISBN 978-0412276309. https://archive.org/details/isbn_9780412276309.
- ↑ 12.0 12.1 Devore, Jay L. (2011). Probability and Statistics for Engineering and the Sciences (8th ed.). Boston, MA: Cengage Learning. pp. 300–344. ISBN 978-0-538-73352-6.
- ↑ Craparo, Robert M. (2007). "Significance level". Encyclopedia of Measurement and Statistics. 3. Thousand Oaks, CA: SAGE Publications. pp. 889–891. ISBN 978-1-412-91611-0.
- ↑ Sproull, Natalie L. (2002). "Hypothesis testing". Handbook of Research Methods: A Guide for Practitioners and Students in the Social Science (2nd ed.). Lanham, MD: Scarecrow Press, Inc.. pp. 49–64. ISBN 978-0-810-84486-5. https://archive.org/details/handbookofresear00spro/page/49.
- ↑ Babbie, Earl R. (2013). "The logic of sampling". The Practice of Social Research (13th ed.). Belmont, CA: Cengage Learning. pp. 185–226. ISBN 978-1-133-04979-1.
- ↑ Faherty, Vincent (2008). "Probability and statistical significance". Compassionate Statistics: Applied Quantitative Analysis for Social Services (With exercises and instructions in SPSS) (1st ed.). Thousand Oaks, CA: SAGE Publications, Inc. pp. 127–138. ISBN 978-1-412-93982-9.
- ↑ McKillup, Steve (2006). "Probability helps you make a decision about your results". Statistics Explained: An Introductory Guide for Life Scientists (1st ed.). Cambridge, United Kingdom: Cambridge University Press. pp. 44–56. ISBN 978-0-521-54316-3. https://archive.org/details/statisticsexplai0000mcki.
- ↑ Myers, Jerome L.; Well, Arnold D.; Lorch, Robert F. Jr. (2010). "The t distribution and its applications". Research Design and Statistical Analysis (3rd ed.). New York, NY: Routledge. pp. 124–153. ISBN 978-0-805-86431-1.
- ↑ 19.0 19.1 Hooper, Peter. "What is P-value?". http://www.stat.ualberta.ca/~hooper/teaching/misc/Pvalue.pdf.
- ↑ Leung, W.-C. (2001-03-01). "Balancing statistical and clinical significance in evaluating treatment effects" (in en). Postgraduate Medical Journal 77 (905): 201–204. doi:10.1136/pmj.77.905.201. ISSN 0032-5473. PMID 11222834.
- ↑ Brian, Éric; Jaisson, Marie (2007). "Physico-Theology and Mathematics (1710–1794)". The Descent of Human Sex Ratio at Birth. Springer Science & Business Media. pp. 1–25. ISBN 978-1-4020-6036-6.
- ↑ John Arbuthnot (1710). "An argument for Divine Providence, taken from the constant regularity observed in the births of both sexes". Philosophical Transactions of the Royal Society of London 27 (325–336): 186–190. doi:10.1098/rstl.1710.0011. http://www.york.ac.uk/depts/maths/histstat/arbuthnot.pdf.
- ↑ Conover, W.J. (1999), "Chapter 3.4: The Sign Test", Practical Nonparametric Statistics (Third ed.), Wiley, pp. 157–176, ISBN 978-0-471-16068-7
- ↑ Sprent, P. (1989), Applied Nonparametric Statistical Methods (Second ed.), Chapman & Hall, ISBN 978-0-412-44980-2
- ↑ Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press. pp. 225–226. ISBN 978-0-67440341-3.
- ↑ Bellhouse, P. (2001), "John Arbuthnot", in Statisticians of the Centuries by C.C. Heyde and E. Seneta, Springer, pp. 39–42, ISBN 978-0-387-95329-8
- ↑ Hald, Anders (1998), "Chapter 4. Chance or Design: Tests of Significance", A History of Mathematical Statistics from 1750 to 1930, Wiley, pp. 65
- ↑ Cumming, Geoff (2011). "From null hypothesis significance to testing effect sizes". Understanding The New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. Multivariate Applications Series. East Sussex, United Kingdom: Routledge. pp. 21–52. ISBN 978-0-415-87968-2.
- ↑ Fisher, Ronald A. (1925). Statistical Methods for Research Workers. Edinburgh, UK: Oliver and Boyd. pp. 43. ISBN 978-0-050-02170-5. https://archive.org/details/statisticalmethoe7fish/page/43.
- ↑ Poletiek, Fenna H. (2001). "Formal theories of testing". Hypothesis-testing Behaviour. Essays in Cognitive Psychology (1st ed.). East Sussex, United Kingdom: Psychology Press. pp. 29–48. ISBN 978-1-841-69159-6.
- ↑ 31.0 31.1 31.2 Quinn, Geoffrey R.; Keough, Michael J. (2002). Experimental Design and Data Analysis for Biologists (1st ed.). Cambridge, UK: Cambridge University Press. pp. 46–69. ISBN 978-0-521-00976-8. https://archive.org/details/experimentaldesi0000quin/page/46.
- ↑ Neyman, J.; Pearson, E.S. (1933). "The testing of statistical hypotheses in relation to probabilities a priori". Mathematical Proceedings of the Cambridge Philosophical Society 29 (4): 492–510. doi:10.1017/S030500410001152X. Bibcode: 1933PCPS...29..492N.
- ↑ "Conclusions about statistical significance are possible with the help of the confidence interval. If the confidence interval does not include the value of zero effect, it can be assumed that there is a statistically significant result." Prel, Jean-Baptist du; Hommel, Gerhard; Röhrig, Bernd; Blettner, Maria (2009). "Confidence Interval or P-Value?". Deutsches Ärzteblatt Online 106 (19): 335–9. doi:10.3238/arztebl.2009.0335. PMID 19547734.
- ↑ StatNews #73: Overlapping Confidence Intervals and Statistical Significance
- ↑ Neyman, J. (1937). "Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability". Philosophical Transactions of the Royal Society A 236 (767): 333–380. doi:10.1098/rsta.1937.0005. Bibcode: 1937RSPTA.236..333N.
- ↑ Meier, Kenneth J.; Brudney, Jeffrey L.; Bohte, John (2011). Applied Statistics for Public and Nonprofit Administration (3rd ed.). Boston, MA: Cengage Learning. pp. 189–209. ISBN 978-1-111-34280-7.
- ↑ Healy, Joseph F. (2009). The Essentials of Statistics: A Tool for Social Research (2nd ed.). Belmont, CA: Cengage Learning. pp. 177–205. ISBN 978-0-495-60143-2.
- ↑ McKillup, Steve (2006). Statistics Explained: An Introductory Guide for Life Scientists (1st ed.). Cambridge, UK: Cambridge University Press. pp. 32–38. ISBN 978-0-521-54316-3. https://archive.org/details/statisticsexplai0000mcki.
- ↑ Health, David (1995). An Introduction To Experimental Design And Statistics For Biology (1st ed.). Boston, MA: CRC press. pp. 123–154. ISBN 978-1-857-28132-3.
- ↑ Hinton, Perry R. (2010). "Significance, error, and power". Statistics explained (3rd ed.). New York, NY: Routledge. pp. 79–90. ISBN 978-1-848-72312-2.
- ↑ Vaughan, Simon (2013). Scientific Inference: Learning from Data (1st ed.). Cambridge, UK: Cambridge University Press. pp. 146–152. ISBN 978-1-107-02482-3.
- ↑ 42.0 42.1 Bracken, Michael B. (2013). Risk, Chance, and Causation: Investigating the Origins and Treatment of Disease (1st ed.). New Haven, CT: Yale University Press. pp. 260–276. ISBN 978-0-300-18884-4. https://archive.org/details/riskchancecausat0000brac.
- ↑ Franklin, Allan (2013). "Prologue: The rise of the sigmas". Shifting Standards: Experiments in Particle Physics in the Twentieth Century (1st ed.). Pittsburgh, PA: University of Pittsburgh Press. pp. Ii–Iii. ISBN 978-0-822-94430-0.
- ↑ Clarke, GM; Anderson, CA; Pettersson, FH; Cardon, LR; Morris, AP; Zondervan, KT (February 6, 2011). "Basic statistical analysis in genetic case-control studies". Nature Protocols 6 (2): 121–33. doi:10.1038/nprot.2010.182. PMID 21293453.
- ↑ Barsh, GS; Copenhaver, GP; Gibson, G; Williams, SM (July 5, 2012). "Guidelines for Genome-Wide Association Studies". PLOS Genetics 8 (7): e1002812. doi:10.1371/journal.pgen.1002812. PMID 22792080.
- ↑ Carver, Ronald P. (1978). "The Case Against Statistical Significance Testing". Harvard Educational Review 48 (3): 378–399. doi:10.17763/haer.48.3.t490261645281841.
- ↑ Ioannidis, John P. A. (2005). "Why most published research findings are false". PLOS Medicine 2 (8): e124. doi:10.1371/journal.pmed.0020124. PMID 16060722.
- ↑ 48.0 48.1 Amrhein, Valentin; Korner-Nievergelt, Fränzi; Roth, Tobias (2017). "The earth is flat (p > 0.05): significance thresholds and the crisis of unreplicable research". PeerJ 5: e3544. doi:10.7717/peerj.3544. PMID 28698825.
- ↑ 49.0 49.1 Hojat, Mohammadreza; Xu, Gang (2004). "A Visitor's Guide to Effect Sizes". Advances in Health Sciences Education 9 (3): 241–9. doi:10.1023/B:AHSE.0000038173.00909.f6. PMID 15316274.
- ↑ Pedhazur, Elazar J.; Schmelkin, Liora P. (1991). Measurement, Design, and Analysis: An Integrated Approach (Student ed.). New York, NY: Psychology Press. pp. 180–210. ISBN 978-0-805-81063-9.
- ↑ Stahel, Werner (2016). "Statistical Issue in Reproducibility". Principles, Problems, Practices, and Prospects Reproducibility: Principles, Problems, Practices, and Prospects: 87–114. doi:10.1002/9781118865064.ch5. ISBN 9781118864975.
- ↑ "CSSME Seminar Series: The argument over p-values and the Null Hypothesis Significance Testing (NHST) paradigm". School of Education, University of Leeds. http://www.education.leeds.ac.uk/events/2015/cssme-seminar-series-the-argument-over-p-values-and-the-null-hypothesis-significance-testing-nhst-paradigm.
- ↑ Novella, Steven (February 25, 2015). "Psychology Journal Bans Significance Testing". Science-Based Medicine. https://www.sciencebasedmedicine.org/psychology-journal-bans-significance-testing.
- ↑ Woolston, Chris (2015-03-05). "Psychology journal bans P values". Nature 519 (7541): 9. doi:10.1038/519009f. Bibcode: 2015Natur.519....9W.
- ↑ Siegfried, Tom (2015-03-17). "P value ban: small step for a journal, giant leap for science". Science News. https://www.sciencenews.org/blog/context/p-value-ban-small-step-journal-giant-leap-science.
- ↑ Antonakis, John (February 2017). "On doing better science: From thrill of discovery to policy implications". The Leadership Quarterly 28 (1): 5–21. doi:10.1016/j.leaqua.2017.01.006. https://serval.unil.ch/resource/serval:BIB_8EF01CB80A64.P001/REF.pdf.
- ↑ 57.0 57.1 57.2 Wasserstein, Ronald L.; Lazar, Nicole A. (2016-04-02). "The ASA's Statement on p-Values: Context, Process, and Purpose". The American Statistician 70 (2): 129–133. doi:10.1080/00031305.2016.1154108. http://revistas.ucm.es/index.php/TEKN/article/view/57194.
- ↑ García-Pérez, Miguel A. (2016-10-05). "Thou Shalt Not Bear False Witness Against Null Hypothesis Significance Testing" (in en). Educational and Psychological Measurement 77 (4): 631–662. doi:10.1177/0013164416668232. ISSN 0013-1644. PMID 30034024.
- ↑ Ioannidis, John P. A.; Ware, Jennifer J.; Wagenmakers, Eric-Jan; Simonsohn, Uri; Chambers, Christopher D.; Button, Katherine S.; Bishop, Dorothy V. M.; Nosek, Brian A. et al. (January 2017). "A manifesto for reproducible science" (in en). Nature Human Behaviour 1: 0021. doi:10.1038/s41562-016-0021. PMID 33954258.
- ↑ Benjamin, Daniel (2018). "Redefine statistical significance". Nature Human Behaviour 1 (1): 6–10. doi:10.1038/s41562-017-0189-z. PMID 30980045.
- ↑ Chawla, Dalmeet (2017). "'One-size-fits-all' threshold for P values under fire". Nature. doi:10.1038/nature.2017.22625. https://www.nature.com/news/one-size-fits-all-threshold-for-p-values-under-fire-1.22625.
- ↑ Amrhein, Valentin; Greenland, Sander (2017). "Remove, rather than redefine, statistical significance". Nature Human Behaviour 2 (1): 0224. doi:10.1038/s41562-017-0224-0. PMID 30980046.
- ↑ Vyse, Stuart (November 2017). "Moving Science's Statistical Goalposts". CSI. https://www.csicop.org/si/show/moving_sciences_statistical_goal_posts.
- ↑ McShane, Blake; Greenland, Sander; Amrhein, Valentin (March 2019). "Scientists rise up against statistical significance" (in EN). Nature 567 (7748): 305–307. doi:10.1038/d41586-019-00857-9. PMID 30894741. Bibcode: 2019Natur.567..305A.
- ↑ Wasserstein, Ronald L.; Schirm, Allen L.; Lazar, Nicole A. (2019-03-20). "Moving to a World Beyond "p < 0.05"". The American Statistician 73 (sup1): 1–19. doi:10.1080/00031305.2019.1583913.
Further reading
- Lydia Denworth, "A Significant Problem: Standard scientific methods are under fire. Will anything change?", Scientific American, vol. 321, no. 4 (October 2019), pp. 62–67. "The use of p values for nearly a century [since 1925] to determine statistical significance of experimental results has contributed to an illusion of certainty and [to] reproducibility crises in many scientific fields. There is growing determination to reform statistical analysis... Some [researchers] suggest changing statistical methods, whereas others would do away with a threshold for defining "significant" results." (p. 63.)
- Ziliak, Stephen and Deirdre McCloskey (2008), The Cult of Statistical Significance: How the Standard Error Costs Us Jobs, Justice, and Lives. Ann Arbor, University of Michigan Press, 2009. ISBN 978-0-472-07007-7. Reviews and reception: (compiled by Ziliak)
- Thompson, Bruce (2004). "The "significance" crisis in psychology and education". Journal of Socio-Economics 33 (5): 607–613. doi:10.1016/j.socec.2004.09.034.
- Chow, Siu L., (1996). Statistical Significance: Rationale, Validity and Utility , Volume 1 of series Introducing Statistical Methods, Sage Publications Ltd, ISBN 978-0-7619-5205-3 – argues that statistical significance is useful in certain circumstances.
- Kline, Rex, (2004). Beyond Significance Testing: Reforming Data Analysis Methods in Behavioral Research Washington, DC: American Psychological Association.
- Nuzzo, Regina (2014). Scientific method: Statistical errors. Nature Vol. 506, p. 150-152 (open access). Highlights common misunderstandings about the p value.
- Cohen, Joseph (1994). [1] . The earth is round (p<.05). American Psychologist. Vol 49, p. 997-1003. Reviews problems with null hypothesis statistical testing.
- Amrhein, Valentin; Greenland, Sander; McShane, Blake (2019-03-20). "Scientists rise up against statistical significance". Nature 567 (7748): 305–307. doi:10.1038/d41586-019-00857-9. PMID 30894741. Bibcode: 2019Natur.567..305A.
External links
- The article "Earliest Known Uses of Some of the Words of Mathematics (S)" contains an entry on Significance that provides some historical information.
- "The Concept of Statistical Significance Testing" (February 1994): article by Bruce Thompon hosted by the ERIC Clearinghouse on Assessment and Evaluation, Washington, D.C.
- "What does it mean for a result to be "statistically significant"?" (no date): an article from the Statistical Assessment Service at George Mason University, Washington, D.C.
 |

