Linear trend estimation

Short description: Statistical technique to aid interpretation of data

Linear trend estimation is a statistical method used to analyze data patterns. When a series of measurements of a process are treated as a sequence or time series, trend estimation can be used to make and justify statements about tendencies in the data by relating the measurements to the times at which they occurred. This model can then be used to describe the behavior of the observed data.

In particular, it is useful to determine if measurements exhibit an increasing or decreasing trend which is statistically distinguished from random behavior. Examples include: determining the trend of the daily average temperatures at a given location from winter to summer; and determining the trend in a global temperature series over the last 100 years. In the latter case, issues of homogeneity are important (for example, knowing whether the series is equally reliable throughout its length).

Fitting a trend: least-squares

Given a set of data and the desire to produce some kind of model of those data, there are a variety of functions that can be chosen for the fit. If there is no prior understanding of the data, then the simplest function is a straight line with the data values on the y axis, and time (t = 1, 2, 3, ...) on the x axis.

The least-squares fit is a common method to fit a straight line through the data. This method minimizes the sum of the squared errors in the data series y.

Given a set of points in time [math]\displaystyle{ t }[/math], and data values [math]\displaystyle{ y_t }[/math] observed for those points in time, values of [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are chosen to minimize the sum of squared errors

[math]\displaystyle{ \sum_t \left[ y_t - \left( \hat{a}t + \hat{b} \right) \right]^2 }[/math]

The values of [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] derived from the data parameterize the simple linear estimator [math]\displaystyle{ \hat{y} = \hat{a} x + \hat{b} }[/math]. The term "trend" refers to the slope [math]\displaystyle{ \hat{a} }[/math] in the least squares estimator.

Trends in random data

Before considering trends in real data, it is useful to understand trends in random data.

Red shaded values are greater than 99% of the rest; blue, 95%; green, 90%. In this case, the V values discussed in the text for (one-sided) 95% confidence is seen to be 0.2.

If a series which is known to be random is analyzed – fair dice falls, or computer-generated pseudo-random numbers – and a trend line is fitted through the data, the chances of an exactly zero estimated trend are negligible. But the trend would be expected to be small. If an individual series of observations is generated from simulations that employ a given variance of noise that equals the observed variance of our data series of interest, and a given length (say, 100 points), a large number of such simulated series (say, 100,000 series) can be generated. These 100,000 series can then be analyzed individually to calculate estimated trends in each series, and these results establish a distribution of estimated trends that are to be expected from such random data – see diagram. Such a distribution will be normal according to the central limit theorem except in pathological cases. A level of statistical certainty, S, may now be selected – 95% confidence is typical; 99% would be stricter, 90% looser – and the following question can be asked: what is the borderline trend value V that would result in S% of trends being between −V and +V?

The above procedure can be replaced by a permutation test. To generate borderline trend values V and −V, the set of 100,000 generated series can be replaced by 100,000 series constructed by randomly shuffling the observed data series. Since such a constructed series would be trend-free, it can be used in a similar way to simulated data.

The distribution of trends was calculated by simulation in the above discussion. In simple cases, such as normally distributed random noise, the distribution of trends can be calculated exactly without simulation.

The range (−V, V) can be used to decide whether a trend estimated from the actual data is unlikely to have come from a data series that truly has a zero trend. If the estimated value of the regression parameter lies outside this range, such a result could have occurred in the presence of a true zero trend only, for example, one time out of twenty if the confidence value S=95% was used. In this case, it can be said that, at degree of certainty S, we reject the null hypothesis that the true underlying trend is zero.

However, note that whatever value of S is chosen, then a given fraction, 1 − S, of truly random series will be declared (falsely, by construction) to have a significant trend. Conversely, a certain fraction of series that in fact have a non-zero trend will not be declared to have a trend.

Data as trend plus noise

To analyze a (time) series of data, it can be assumed that it may be represented as trend plus noise:

[math]\displaystyle{ y_t = at + b + e_t\, }[/math]

where [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are unknown constants and the [math]\displaystyle{ e }[/math]'s are randomly distributed errors. If one can reject the null hypothesis that the errors are non-stationary, then the non-stationary series {y_t } is called trend-stationary. The least squares method assumes the errors to be independently distributed with a normal distribution. If this is not the case, hypothesis tests about the unknown parameters a and b may be inaccurate. It is simplest if the [math]\displaystyle{ e }[/math]'s all have the same distribution, but if not (if some have higher variance, meaning that those data points are effectively less certain) then this can be taken into account during the least squares fitting, by weighting each point by the inverse of the variance of that point.

In most cases, where only a single time series exists to be analyzed, the variance of the [math]\displaystyle{ e }[/math]'s is estimated by fitting a trend to obtain the estimated parameter values [math]\displaystyle{ \hat a }[/math] and [math]\displaystyle{ \hat b, }[/math] thus allowing the predicted values

[math]\displaystyle{ \hat y =\hat at+\hat b }[/math]

to be subtracted from the data [math]\displaystyle{ y_t }[/math] (thus detrending the data) and leaving the residuals [math]\displaystyle{ \hat e_t }[/math] as the detrended data, and estimating the variance of the [math]\displaystyle{ e_t }[/math]'s from the residuals — this is often the only way of estimating the variance of the [math]\displaystyle{ e_t }[/math]'s.

Once the "noise" of the series is known, the significance of the trend can be assessed by making the null hypothesis that the trend, [math]\displaystyle{ a }[/math], is not different from 0. From the above discussion of trends in random data with known variance, the distribution of calculated trends is to be expected from random (trendless) data. If the estimated trend, [math]\displaystyle{ \hat a }[/math], is larger than the critical value for a certain significance level, then the estimated trend is deemed significantly different from zero at that significance level, and the null hypothesis of zero underlying trend is rejected.

The use of a linear trend line has been the subject of criticism, leading to a search for alternative approaches to avoid its use in model estimation. One of the alternative approaches involves unit root tests and the cointegration technique in econometric studies.

The estimated coefficient associated with a linear trend variable such as time is interpreted as a measure of the impact of a number of unknown or known but unmeasurable factors on the dependent variable over one unit of time. Strictly speaking, that interpretation is applicable for the estimation time frame only. Outside that time frame, one does not know how those unmeasurable factors behave both qualitatively and quantitatively. Furthermore, the linearity of the time trend poses many questions:

1. Why should it be linear?

2. If the trend is non-linear then under what conditions does its inclusion influence the magnitude as well as the statistical significance of the estimates of other parameters in the model?

3. The inclusion of a linear time trend in a model precludes by assumption the presence of fluctuations in the tendencies of the dependent variable over time; is this necessarily valid in a particular context?

4. And, does a spurious relationship exist in the model because an underlying causative variable is itself time-trending?

Research results of mathematicians, statisticians, econometricians, and economists have been published in response to those questions. For example, detailed notes on the meaning of linear time trends in regression model are given in Cameron (2005); Granger, Engle and many other econometricians have written on stationarity, unit root testing, co-integration and related issues (a summary of some of the works in this area can be found in an information paper by the Royal Swedish Academy of Sciences (2003); and Ho-Trieu & Tucker (1990) have written on logarithmic time trends with results indicating linear time trends are special cases of cycles.

Example: noisy time series

It is harder to see a trend in a noisy time series. For example, if the true series is 0, 1, 2, 3 all plus some independent normally distributed "noise" e of standard deviation E, and a sample series of length 50 is given, then if E = 0.1 the trend will be obvious; if E = 100 the trend will probably be visible; but if E = 10000 the trend will be buried in the noise.

Consider a concrete example, such as the global surface temperature record of the past 140 years as presented by the IPCC: then the interannual variation is about 0.2 °C and the trend about 0.6 °C over 140 years, with 95% confidence limits of 0.2 °C (by coincidence, about the same value as the interannual variation). Hence the trend is statistically different from 0. However, as noted elsewhere this time series doesn't conform to the assumptions necessary for least squares to be valid.

Goodness of fit (r-squared) and trend

Illustration of the effect of filtering on r². Black = unfiltered data; red = data averaged every 10 points; blue = data averaged every 100 points. All have the same trend, but more filtering leads to higher r² of fitted trend line.

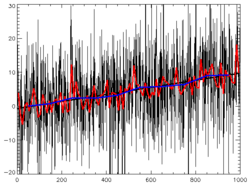
The least-squares fitting process produces a value – r-squared (r²) – which is 1 minus the ratio of the variance of the residuals to the variance of the dependent variable. It says what fraction of the variance of the data is explained by the fitted trend line. It does not relate to the statistical significance of the trend line (see graph); statistical significance of the trend is determined by its t-statistic. Often, filtering a series increases r² while making little difference to the fitted trend.

Real data may need more complicated models

Thus far the data have been assumed to consist of the trend plus noise, with the noise at each data point being independent and identically distributed random variables and to have a normal distribution. Real data (for example climate data) may not fulfill these criteria. This is important, as it makes an enormous difference to the ease with which the statistics can be analysed so as to extract maximum information from the data series. If there are other non-linear effects that have a correlation to the independent variable (such as cyclic influences), the use of least-squares estimation of the trend is not valid. Also where the variations are significantly larger than the resulting straight line trend, the choice of start and end points can significantly change the result. That is, the model is mathematically misspecified. Statistical inferences (tests for the presence of trend, confidence intervals for the trend, etc.) are invalid unless departures from the standard assumptions are properly accounted for, for example as follows:

• Dependence: autocorrelated time series might be modeled using autoregressive moving average models.
• Non-constant variance: in the simplest cases weighted least squares might be used.
• Non-normal distribution for errors: in the simplest cases a generalised linear model might be applicable.
• Unit root: taking first (or occasionally second) differences of the data, with the level of differencing being identified through various unit root tests.

In R, the linear trend in data can be estimated by using the 'tslm' function of the 'forecast' package.

Trends in clinical data

Medical and biomedical studies often seek to determine a link in sets of data, such as (as indicated above) three different diseases. But data may also be linked in time (such as change in the effect of a drug from baseline, to month 1, to month 2), or by an external factor that may or may not be determined by the researcher and/or their subject (such as no pain, mild pain, moderate pain, severe pain). In these cases one would expect the effect test statistic (e.g. influence of a statin on levels of cholesterol, an analgesic on the degree of pain, or increasing doses of a drug on a measurable index) to change in direct order as the effect develops. Suppose the mean level of cholesterol before and after the prescription of a statin falls from 5.6 mmol/L at baseline to 3.4 mmol/L at one month and to 3.7 mmol/L at two months. Given sufficient power, an ANOVA would most likely find a significant fall at one and two months, but the fall is not linear. Furthermore, a post-hoc test may be required. An alternative test may be repeated measures (two way) ANOVA, or Friedman test, depending on the nature of the data. Nevertheless, because the groups are ordered, a standard ANOVA is inappropriate. Should the cholesterol fall from 5.4 to 4.1 to 3.7, there is a clear linear trend. The same principal may be applied to the effects of allele/genotype frequency, where it could be argued that SNPs in nucleotides XX, XY, YY are in fact a trend of no Y's, one Y, and then two Y's.

The mathematics of linear trend estimation is a variant of the standard ANOVA, giving different information, and would be the most appropriate test if the researchers are hypothesising a trend effect in their test statistic. One example is of levels of serum trypsin in six groups of subjects ordered by age decade (10–19 years up to 60–69 years). Levels of trypsin (ng/mL) rise in a direct linear trend of 128, 152, 194, 207, 215, 218. Unsurprisingly, a 'standard' ANOVA gives p < 0.0001, whereas linear trend estimation give p = 0.00006. Incidentally, it could be reasonably argued that as age is a natural continuously variable index, it should not be categorised into decades, and an effect of age and serum trypsin sought by correlation (assuming the raw data is available). A further example is of a substance measured at four time points in different groups:

#	mean	SD
1	1.6	0.56
2	1.94	0.75
3	2.22	0.66
4	2.40	0.79

This is a clear trend. ANOVA gives p = 0.091, because the overall variance exceeds the means, whereas linear trend estimation gives p = 0.012. However, should the data have been collected at four time points in the same individuals, linear trend estimation would be inappropriate, and a two-way (repeated measures) ANOVA applied.

See also

• Estimation
• Extrapolation
• Forecasting
• Least squares
• Least-squares spectral analysis
• Line fitting
• Prediction interval
• Regression analysis

References

• Bianchi, M.; Boyle, M.; Hollingsworth, D. (1999). "A comparison of methods for trend estimation". Applied Economics Letters 6 (2): 103–109. doi:10.1080/135048599353726. 
• Cameron, S. (2005). "Making Regression Analysis More Useful, II". Econometrics. Maidenhead: McGraw Hill Higher Education. pp. 171–198. ISBN 0077104285. 
• Chatfield, C. (1993). "Calculating Interval Forecasts". Journal of Business and Economic Statistics 11 (2): 121–135. doi:10.1080/07350015.1993.10509938. 
• Ho-Trieu, N. L.; Tucker, J. (1990). "Another note on the use of a logarithmic time trend". Review of Marketing and Agricultural Economics 58 (1): 89–90. doi:10.22004/ag.econ.12288. 
• Kungl. Vetenskapsakademien (2003). "Time-series econometrics: Cointegration and autoregressive conditional heteroskedasticity". Advanced Information on the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel (The Royal Swedish Academy of Sciences). 
• Arianos, S.; Carbone, A.; Turk, C. (2011). "Self-similarity of high-order moving averages". Physical Review E 84 (4): 046113. doi:10.1103/physreve.84.046113. PMID 22181233. Bibcode: 2011PhRvE..84d6113A. http://porto.polito.it/2488907/.