Physics:Zero-point energy

| Part of a series on |
| Quantum mechanics |
|---|
| [math]\displaystyle{ i \hbar \frac{\partial}{\partial t} | \psi (t) \rangle = \hat{H} | \psi (t) \rangle }[/math] |
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.[1] Therefore, even at absolute zero, atoms and molecules retain some vibrational motion. Apart from atoms and molecules, the empty space of the vacuum also has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions (i.e., leptons and quarks), and force fields, whose quanta are bosons (e.g., photons and gluons). All these fields have zero-point energy.[2] These fluctuating zero-point fields lead to a kind of reintroduction of an aether in physics[1][3] since some systems can detect the existence of this energy. However, this aether cannot be thought of as a physical medium if it is to be Lorentz invariant such that there is no contradiction with Einstein's theory of special relativity.[1]
The notion of a zero-point energy is also important for cosmology, and physics currently lacks a full theoretical model for understanding zero-point energy in this context; in particular, the discrepancy between theorized and observed vacuum energy in the universe is a source of major contention.[4] Physicists Richard Feynman and John Wheeler calculated the zero-point radiation of the vacuum to be an order of magnitude greater than nuclear energy, with a single light bulb containing enough energy to boil all the world's oceans.[citation needed] Yet according to Einstein's theory of general relativity, any such energy would gravitate, and the experimental evidence from the expansion of the universe, dark energy and the Casimir effect shows any such energy to be exceptionally weak. A popular proposal that attempts to address this issue is to say that the fermion field has a negative zero-point energy, while the boson field has positive zero-point energy and thus these energies somehow cancel each other out.[5][6] This idea would be true if supersymmetry were an exact symmetry of nature; however, the LHC at CERN has so far found no evidence to support it. Moreover, it is known that if supersymmetry is valid at all, it is at most a broken symmetry, only true at very high energies, and no one has been able to show a theory where zero-point cancellations occur in the low-energy universe we observe today.[6] This discrepancy is known as the cosmological constant problem and it is one of the greatest unsolved mysteries in physics. Many physicists believe that "the vacuum holds the key to a full understanding of nature".[7]
Etymology and terminology
The term zero-point energy (ZPE) is a translation from the German Nullpunktsenergie.[8] Sometimes used interchangeably with it are the terms zero-point radiation and ground state energy. The term zero-point field (ZPF) can be used when referring to a specific vacuum field, for instance the QED vacuum which specifically deals with quantum electrodynamics (e.g., electromagnetic interactions between photons, electrons and the vacuum) or the QCD vacuum which deals with quantum chromodynamics (e.g., color charge interactions between quarks, gluons and the vacuum). A vacuum can be viewed not as empty space but as the combination of all zero-point fields. In quantum field theory this combination of fields is called the vacuum state, its associated zero-point energy is called the vacuum energy and the average energy value is called the vacuum expectation value (VEV) also called its condensate.
Overview
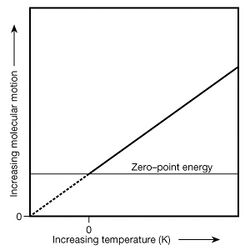
In classical mechanics all particles can be thought of as having some energy made up of their potential energy and kinetic energy. Temperature, for example, arises from the intensity of random particle motion caused by kinetic energy (known as Brownian motion). As temperature is reduced to absolute zero, it might be thought that all motion ceases and particles come completely to rest. In fact, however, kinetic energy is retained by particles even at the lowest possible temperature. The random motion corresponding to this zero-point energy never vanishes; it is a consequence of the uncertainty principle of quantum mechanics.
The uncertainty principle states that no object can ever have precise values of position and velocity simultaneously. The total energy of a quantum mechanical object (potential and kinetic) is described by its Hamiltonian which also describes the system as a harmonic oscillator, or wave function, that fluctuates between various energy states (see wave-particle duality). All quantum mechanical systems undergo fluctuations even in their ground state, a consequence of their wave-like nature. The uncertainty principle requires every quantum mechanical system to have a fluctuating zero-point energy greater than the minimum of its classical potential well. This results in motion even at absolute zero. For example, liquid helium does not freeze under atmospheric pressure regardless of temperature due to its zero-point energy.
Given the equivalence of mass and energy expressed by Albert Einstein's E = mc2, any point in space that contains energy can be thought of as having mass to create particles. Virtual particles spontaneously flash into existence at every point in space due to the energy of quantum fluctuations caused by the uncertainty principle. Modern physics has developed quantum field theory (QFT) to understand the fundamental interactions between matter and forces, it treats every single point of space as a quantum harmonic oscillator. According to QFT the universe is made up of matter fields, whose quanta are fermions (i.e. leptons and quarks), and force fields, whose quanta are bosons (e.g. photons and gluons). All these fields have zero-point energy.[2] Recent experiments advocate the idea that particles themselves can be thought of as excited states of the underlying quantum vacuum, and that all properties of matter are merely vacuum fluctuations arising from interactions of the zero-point field.[9]
The idea that "empty" space can have an intrinsic energy associated with it, and that there is no such thing as a "true vacuum" is seemingly unintuitive. It is often argued that the entire universe is completely bathed in the zero-point radiation, and as such it can add only some constant amount to calculations. Physical measurements will therefore reveal only deviations from this value.[10] For many practical calculations zero-point energy is dismissed by fiat in the mathematical model as a term that has no physical effect. Such treatment causes problems however, as in Einstein's theory of general relativity the absolute energy value of space is not an arbitrary constant and gives rise to the cosmological constant. For decades most physicists assumed that there was some undiscovered fundamental principle that will remove the infinite zero-point energy and make it completely vanish. If the vacuum has no intrinsic, absolute value of energy it will not gravitate. It was believed that as the universe expands from the aftermath of the Big Bang, the energy contained in any unit of empty space will decrease as the total energy spreads out to fill the volume of the universe; galaxies and all matter in the universe should begin to decelerate. This possibility was ruled out in 1998 by the discovery that the expansion of the universe is not slowing down but is in fact accelerating, meaning empty space does indeed have some intrinsic energy. The discovery of dark energy is best explained by zero-point energy, though it still remains a mystery as to why the value appears to be so small compared to the huge value obtained through theory – the cosmological constant problem.[5]
Many physical effects attributed to zero-point energy have been experimentally verified, such as spontaneous emission, Casimir force, Lamb shift, magnetic moment of the electron and Delbrück scattering.[11][12] These effects are usually called "radiative corrections".[13] In more complex nonlinear theories (e.g. QCD) zero-point energy can give rise to a variety of complex phenomena such as multiple stable states, symmetry breaking, chaos and emergence. Many physicists believe that "the vacuum holds the key to a full understanding of nature"[7] and that studying it is critical in the search for the theory of everything. Active areas of research include the effects of virtual particles,[14] quantum entanglement,[15] the difference (if any) between inertial and gravitational mass,[16] variation in the speed of light,[17] a reason for the observed value of the cosmological constant[18] and the nature of dark energy.[19][20]
History
Early aether theories
Zero-point energy evolved from historical ideas about the vacuum. To Aristotle the vacuum was τὸ κενόν, "the empty"; i.e., space independent of body. He believed this concept violated basic physical principles and asserted that the elements of fire, air, earth, and water were not made of atoms, but were continuous. To the atomists the concept of emptiness had absolute character: it was the distinction between existence and nonexistence.[21] Debate about the characteristics of the vacuum were largely confined to the realm of philosophy, it was not until much later on with the beginning of the renaissance, that Otto von Guericke invented the first vacuum pump and the first testable scientific ideas began to emerge. It was thought that a totally empty volume of space could be created by simply removing all gases. This was the first generally accepted concept of the vacuum.[22]
Late in the 19th century, however, it became apparent that the evacuated region still contained thermal radiation. The existence of the aether as a substitute for a true void was the most prevalent theory of the time. According to the successful electromagnetic aether theory based upon Maxwell's electrodynamics, this all-encompassing aether was endowed with energy and hence very different from nothingness. The fact that electromagnetic and gravitational phenomena were easily transmitted in empty space indicated that their associated aethers were part of the fabric of space itself. Maxwell himself noted that:
To those who maintained the existence of a plenum as a philosophical principle, nature's abhorrence of a vacuum was a sufficient reason for imagining an all-surrounding aether ... Aethers were invented for the planets to swim in, to constitute electric atmospheres and magnetic effluvia, to convey sensations from one part of our bodies to another, and so on, till a space had been filled three or four times with aethers.[23]
However, the results of the Michelson–Morley experiment in 1887 were the first strong evidence that the then-prevalent aether theories were seriously flawed, and initiated a line of research that eventually led to special relativity, which ruled out the idea of a stationary aether altogether. To scientists of the period, it seemed that a true vacuum in space might be created by cooling and thus eliminating all radiation or energy. From this idea evolved the second concept of achieving a real vacuum: cool a region of space down to absolute zero temperature after evacuation. Absolute zero was technically impossible to achieve in the 19th century, so the debate remained unsolved.
Second quantum theory
In 1900, Max Planck derived the average energy ε of a single energy radiator, e.g., a vibrating atomic unit, as a function of absolute temperature:[24]
[math]\displaystyle{ \varepsilon = \frac{h\nu}{ e^{h\nu/(kT)}-1} \,, }[/math]
where h is Planck's constant, ν is the frequency, k is the Boltzmann constant, and T is the absolute temperature. The zero-point energy makes no contribution to Planck's original law, as its existence was unknown to Planck in 1900.[25]
The concept of zero-point energy was developed by Max Planck in Germany in 1911 as a corrective term added to a zero-grounded formula developed in his original quantum theory in 1900.[26]
In 1912, Max Planck published the first journal article to describe the discontinuous emission of radiation, based on the discrete quanta of energy.[27] In Planck's "second quantum theory" resonators absorbed energy continuously, but emitted energy in discrete energy quanta only when they reached the boundaries of finite cells in phase space, where their energies became integer multiples of hν. This theory led Planck to his new radiation law, but in this version energy resonators possessed a zero-point energy, the smallest average energy a resonator could take on. Planck's radiation equation contained a residual energy factor, one hν/2, as an additional term dependent on the frequency ν, which was greater than zero (where h is Planck's constant). It is therefore widely agreed that "Planck's equation marked the birth of the concept of zero-point energy."[28] In a series of papers from 1911 to 1913,[29] Planck found the average energy of an oscillator to be:[26][30]
[math]\displaystyle{ \varepsilon =\frac{h\nu} 2 + \frac{h\nu}{e^{h\nu/(kT)}-1} ~. }[/math]
Soon, the idea of zero-point energy attracted the attention of Albert Einstein and his assistant Otto Stern.[31] In 1913 they published a paper that attempted to prove the existence of zero-point energy by calculating the specific heat of hydrogen gas and compared it with the experimental data. However, after assuming they had succeeded, they retracted support for the idea shortly after publication because they found Planck's second theory may not apply to their example. In a letter to Paul Ehrenfest of the same year Einstein declared zero-point energy "dead as a doornail".[32] Zero-point energy was also invoked by Peter Debye,[33] who noted that zero-point energy of the atoms of a crystal lattice would cause a reduction in the intensity of the diffracted radiation in X-ray diffraction even as the temperature approached absolute zero. In 1916 Walther Nernst proposed that empty space was filled with zero-point electromagnetic radiation.[34] With the development of general relativity Einstein found the energy density of the vacuum to contribute towards a cosmological constant in order to obtain static solutions to his field equations; the idea that empty space, or the vacuum, could have some intrinsic energy associated with it had returned, with Einstein stating in 1920:
There is a weighty argument to be adduced in favour of the aether hypothesis. To deny the aether is ultimately to assume that empty space has no physical qualities whatever. The fundamental facts of mechanics do not harmonize with this view ... according to the general theory of relativity space is endowed with physical qualities; in this sense, therefore, there exists an aether. According to the general theory of relativity space without aether is unthinkable; for in such space there not only would be no propagation of light, but also no possibility of existence for standards of space and time (measuring-rods and clocks), nor therefore any space-time intervals in the physical sense. But this aether may not be thought of as endowed with the quality characteristic of ponderable media, as consisting of parts which may be tracked through time. The idea of motion may not be applied to it.[35][36]
Kurt Bennewitz (de) and Francis Simon (1923),[37] who worked at Walther Nernst's laboratory in Berlin, studied the melting process of chemicals at low temperatures. Their calculations of the melting points of hydrogen, argon and mercury led them to conclude that the results provided evidence for a zero-point energy. Moreover, they suggested correctly, as was later verified by Simon (1934),[38][39] that this quantity was responsible for the difficulty in solidifying helium even at absolute zero. In 1924 Robert Mulliken[40] provided direct evidence for the zero-point energy of molecular vibrations by comparing the band spectrum of 10BO and 11BO: the isotopic difference in the transition frequencies between the ground vibrational states of two different electronic levels would vanish if there were no zero-point energy, in contrast to the observed spectra. Then just a year later in 1925,[41] with the development of matrix mechanics in Werner Heisenberg's famous article "Quantum theoretical re-interpretation of kinematic and mechanical relations" the zero-point energy was derived from quantum mechanics.[42]
In 1913 Niels Bohr had proposed what is now called the Bohr model of the atom,[43][44][45] but despite this it remained a mystery as to why electrons do not fall into their nuclei. According to classical ideas, the fact that an accelerating charge loses energy by radiating implied that an electron should spiral into the nucleus and that atoms should not be stable. This problem of classical mechanics was nicely summarized by James Hopwood Jeans in 1915: "There would be a very real difficulty in supposing that the (force) law 1/r2 held down to the zero values of r. For the forces between two charges at zero distance would be infinite; we should have charges of opposite sign continually rushing together and, when once together, no force would tend to shrink into nothing or to diminish indefinitely in size."[46] The resolution to this puzzle came in 1926 with Schrödinger's famous equation.[47] This equation explained the new, non-classical fact that an electron confined to be close to a nucleus would necessarily have a large kinetic energy so that the minimum total energy (kinetic plus potential) actually occurs at some positive separation rather than at zero separation; in other words, zero-point energy is essential for atomic stability.[48]
Quantum field theory and beyond
In 1926 Pascual Jordan[49] published the first attempt to quantize the electromagnetic field. In a joint paper with Max Born and Werner Heisenberg he considered the field inside a cavity as a superposition of quantum harmonic oscillators. In his calculation he found that in addition to the "thermal energy" of the oscillators there also had to exist an infinite zero-point energy term. He was able to obtain the same fluctuation formula that Einstein had obtained in 1909.[50] However, Jordan did not think that his infinite zero-point energy term was "real", writing to Einstein that "it is just a quantity of the calculation having no direct physical meaning".[51] Jordan found a way to get rid of the infinite term, publishing a joint work with Pauli in 1928,[52] performing what has been called "the first infinite subtraction, or renormalisation, in quantum field theory".[53]
Building on the work of Heisenberg and others, Paul Dirac's theory of emission and absorption (1927)[54] was the first application of the quantum theory of radiation. Dirac's work was seen as crucially important to the emerging field of quantum mechanics; it dealt directly with the process in which "particles" are actually created: spontaneous emission.[55] Dirac described the quantization of the electromagnetic field as an ensemble of harmonic oscillators with the introduction of the concept of creation and annihilation operators of particles. The theory showed that spontaneous emission depends upon the zero-point energy fluctuations of the electromagnetic field in order to get started.[56][57] In a process in which a photon is annihilated (absorbed), the photon can be thought of as making a transition into the vacuum state. Similarly, when a photon is created (emitted), it is occasionally useful to imagine that the photon has made a transition out of the vacuum state. In the words of Dirac:[54]
The light-quantum has the peculiarity that it apparently ceases to exist when it is in one of its stationary states, namely, the zero state, in which its momentum and therefore also its energy, are zero. When a light-quantum is absorbed it can be considered to jump into this zero state, and when one is emitted it can be considered to jump from the zero state to one in which it is physically in evidence, so that it appears to have been created. Since there is no limit to the number of light-quanta that may be created in this way, we must suppose that there are an infinite number of light quanta in the zero state ...
Contemporary physicists, when asked to give a physical explanation for spontaneous emission, generally invoke the zero-point energy of the electromagnetic field. This view was popularized by Victor Weisskopf who in 1935 wrote:[58]
From quantum theory there follows the existence of so called zero-point oscillations; for example each oscillator in its lowest is not completely at rest but always is moving about its equilibrium position. Therefore electromagnetic oscillations also can never cease completely. Thus the quantum nature of the electromagnetic field has as its consequence zero point oscillations of the field strength in the lowest energy state, in which there are no light quanta in space ... The zero point oscillations act on an electron in the same way as ordinary electrical oscillations do. They can change the eigenstate of the electron, but only in a transition to a state with the lowest energy, since empty space can only take away energy, and not give it up. In this way spontaneous radiation arises as a consequence of the existence of these unique field strengths corresponding to zero point oscillations. Thus spontaneous radiation is induced radiation of light quanta produced by zero point oscillations of empty space
This view was also later supported by Theodore Welton (de) (1948),[59] who argued that spontaneous emission "can be thought of as forced emission taking place under the action of the fluctuating field". This new theory, which Dirac coined quantum electrodynamics (QED), predicted a fluctuating zero-point or "vacuum" field existing even in the absence of sources.
Throughout the 1940s improvements in microwave technology made it possible to take more precise measurements of the shift of the levels of a hydrogen atom, now known as the Lamb shift,[60] and measurement of the magnetic moment of the electron.[61] Discrepancies between these experiments and Dirac's theory led to the idea of incorporating renormalisation into QED to deal with zero-point infinities. Renormalization was originally developed by Hans Kramers[62] and also Victor Weisskopf (1936),[63] and first successfully applied to calculate a finite value for the Lamb shift by Hans Bethe (1947).[64] As per spontaneous emission, these effects can in part be understood with interactions with the zero-point field.[65][11] But in light of renormalisation being able to remove some zero-point infinities from calculations, not all physicists were comfortable attributing zero-point energy any physical meaning, viewing it instead as a mathematical artifact that might one day be eliminated. In Wolfgang Pauli's 1945 Nobel lecture[66] he made clear his opposition to the idea of zero-point energy stating "It is clear that this zero-point energy has no physical reality".
In 1948 Hendrik Casimir[67][68] showed that one consequence of the zero-point field is an attractive force between two uncharged, perfectly conducting parallel plates, the so-called Casimir effect. At the time, Casimir was studying the properties of colloidal solutions. These are viscous materials, such as paint and mayonnaise, that contain micron-sized particles in a liquid matrix. The properties of such solutions are determined by Van der Waals forces – short-range, attractive forces that exist between neutral atoms and molecules. One of Casimir's colleagues, Theo Overbeek, realized that the theory that was used at the time to explain Van der Waals forces, which had been developed by Fritz London in 1930,[69][70] did not properly explain the experimental measurements on colloids. Overbeek therefore asked Casimir to investigate the problem. Working with Dirk Polder, Casimir discovered that the interaction between two neutral molecules could be correctly described only if the fact that light travels at a finite speed was taken into account.[71] Soon afterwards after a conversation with Bohr about zero-point energy, Casimir noticed that this result could be interpreted in terms of vacuum fluctuations. He then asked himself what would happen if there were two mirrors – rather than two molecules – facing each other in a vacuum. It was this work that led to his famous prediction of an attractive force between reflecting plates. The work by Casimir and Polder opened up the way to a unified theory of van der Waals and Casimir forces and a smooth continuum between the two phenomena. This was done by Lifshitz (1956)[72][73][74] in the case of plane parallel dielectric plates. The generic name for both van der Waals and Casimir forces is dispersion forces, because both of them are caused by dispersions of the operator of the dipole moment.[75] The role of relativistic forces becomes dominant at orders of a hundred nanometers.
In 1951 Herbert Callen and Theodore Welton[76] proved the quantum fluctuation-dissipation theorem (FDT) which was originally formulated in classical form by Nyquist (1928)[77] as an explanation for observed Johnson noise in electric circuits.[78] The fluctuation-dissipation theorem showed that when something dissipates energy, in an effectively irreversible way, a connected heat bath must also fluctuate. The fluctuations and the dissipation go hand in hand; it is impossible to have one without the other. The implication of FDT being that the vacuum could be treated as a heat bath coupled to a dissipative force and as such energy could, in part, be extracted from the vacuum for potentially useful work.[79] FDT has been shown to be true experimentally under certain quantum, non-classical, conditions.[80][81][82]
In 1963 the Jaynes–Cummings model[83] was developed describing the system of a two-level atom interacting with a quantized field mode (i.e. the vacuum) within an optical cavity. It gave nonintuitive predictions such as that an atom's spontaneous emission could be driven by field of effectively constant frequency (Rabi frequency). In the 1970s experiments were being performed to test aspects of quantum optics and showed that the rate of spontaneous emission of an atom could be controlled using reflecting surfaces.[84][85] These results were at first regarded with suspicion in some quarters: it was argued that no modification of a spontaneous emission rate would be possible, after all, how can the emission of a photon be affected by an atom's environment when the atom can only "see" its environment by emitting a photon in the first place? These experiments gave rise to cavity quantum electrodynamics (CQED), the study of effects of mirrors and cavities on radiative corrections. Spontaneous emission can be suppressed (or "inhibited")[86][87] or amplified. Amplification was first predicted by Purcell in 1946[88] (the Purcell effect) and has been experimentally verified.[89] This phenomenon can be understood, partly, in terms of the action of the vacuum field on the atom.[90]
The uncertainty principle
Zero-point energy is fundamentally related to the Heisenberg uncertainty principle.[91] Roughly speaking, the uncertainty principle states that complementary variables (such as a particle's position and momentum, or a field's value and derivative at a point in space) cannot simultaneously be specified precisely by any given quantum state. In particular, there cannot exist a state in which the system simply sits motionless at the bottom of its potential well, for then its position and momentum would both be completely determined to arbitrarily great precision. Therefore, the lowest-energy state (the ground state) of the system must have a distribution in position and momentum that satisfies the uncertainty principle, which implies its energy must be greater than the minimum of the potential well.
Near the bottom of a potential well, the Hamiltonian of a general system (the quantum-mechanical operator giving its energy) can be approximated as a quantum harmonic oscillator,
[math]\displaystyle{ \hat{H} = V_0 + \tfrac{1}{2} k \left(\hat{x} - x_0\right)^2 + \frac{1}{2m} \hat{p}^2 \,, }[/math] where V0 is the minimum of the classical potential well.
The uncertainty principle tells us that
[math]\displaystyle{ \sqrt{\left\langle \left(\hat{x} - x_0\right)^2 \right\rangle} \sqrt{\left\langle \hat{p}^2 \right\rangle} \geq \frac{\hbar}{2} \,, }[/math]
making the expectation values of the kinetic and potential terms above satisfy
[math]\displaystyle{ \left\langle \tfrac{1}{2} k \left(\hat{x} - x_0\right)^2 \right\rangle \left\langle \frac{1}{2m} \hat{p}^2 \right\rangle \geq \left(\frac{\hbar}{4}\right)^2 \frac{k}{m} \,. }[/math]
The expectation value of the energy must therefore be at least
[math]\displaystyle{ \left\langle \hat{H} \right\rangle \geq V_0 + \frac{\hbar}{2} \sqrt{\frac{k}{m}} = V_0 + \frac{\hbar \omega}{2} }[/math]
where ω = √k/m is the angular frequency at which the system oscillates.
A more thorough treatment, showing that the energy of the ground state actually saturates this bound and is exactly E0 = V0 + ħω/2, requires solving for the ground state of the system.
Atomic physics
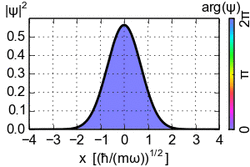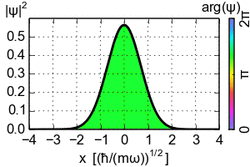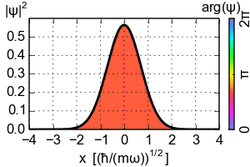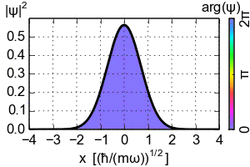
The idea of a quantum harmonic oscillator and its associated energy can apply to either an atom or a subatomic particle. In ordinary atomic physics, the zero-point energy is the energy associated with the ground state of the system. The professional physics literature tends to measure frequency, as denoted by ν above, using angular frequency, denoted with ω and defined by ω = 2πν. This leads to a convention of writing Planck's constant h with a bar through its top (ħ) to denote the quantity h/2π. In these terms, the most famous such example of zero-point energy is the above E = ħω/2 associated with the ground state of the quantum harmonic oscillator. In quantum mechanical terms, the zero-point energy is the expectation value of the Hamiltonian of the system in the ground state.
If more than one ground state exists, they are said to be degenerate. Many systems have degenerate ground states. Degeneracy occurs whenever there exists a unitary operator which acts non-trivially on a ground state and commutes with the Hamiltonian of the system.
According to the third law of thermodynamics, a system at absolute zero temperature exists in its ground state; thus, its entropy is determined by the degeneracy of the ground state. Many systems, such as a perfect crystal lattice, have a unique ground state and therefore have zero entropy at absolute zero. It is also possible for the highest excited state to have absolute zero temperature for systems that exhibit negative temperature.
The wave function of the ground state of a particle in a one-dimensional well is a half-period sine wave which goes to zero at the two edges of the well. The energy of the particle is given by:
[math]\displaystyle{ \frac{h^2 n^2}{8 m L^2} }[/math]
where h is the Planck constant, m is the mass of the particle, n is the energy state (n = 1 corresponds to the ground-state energy), and L is the width of the well.
Quantum field theory
| Quantum field theory |
|---|
 |
| History |
In quantum field theory (QFT), the fabric of "empty" space is visualized as consisting of fields, with the field at every point in space and time being a quantum harmonic oscillator, with neighboring oscillators interacting with each other. According to QFT the universe is made up of matter fields whose quanta are fermions (e.g. electrons and quarks), force fields whose quanta are bosons (i.e. photons and gluons) and a Higgs field whose quantum is the Higgs boson. The matter and force fields have zero-point energy.[2] A related term is zero-point field (ZPF), which is the lowest energy state of a particular field.[92] The vacuum can be viewed not as empty space, but as the combination of all zero-point fields.
In QFT the zero-point energy of the vacuum state is called the vacuum energy and the average expectation value of the Hamiltonian is called the vacuum expectation value (also called condensate or simply VEV). The QED vacuum is a part of the vacuum state which specifically deals with quantum electrodynamics (e.g. electromagnetic interactions between photons, electrons and the vacuum) and the QCD vacuum deals with quantum chromodynamics (e.g. color charge interactions between quarks, gluons and the vacuum). Recent experiments advocate the idea that particles themselves can be thought of as excited states of the underlying quantum vacuum, and that all properties of matter are merely vacuum fluctuations arising from interactions with the zero-point field.[9]
Each point in space makes a contribution of E = ħω/2, resulting in a calculation of infinite zero-point energy in any finite volume; this is one reason renormalization is needed to make sense of quantum field theories. In cosmology, the vacuum energy is one possible explanation for the cosmological constant[18] and the source of dark energy.[19][20]
Scientists are not in agreement about how much energy is contained in the vacuum. Quantum mechanics requires the energy to be large as Paul Dirac claimed it is, like a sea of energy. Other scientists specializing in General Relativity require the energy to be small enough for curvature of space to agree with observed astronomy. The Heisenberg uncertainty principle allows the energy to be as large as needed to promote quantum actions for a brief moment of time, even if the average energy is small enough to satisfy relativity and flat space. To cope with disagreements, the vacuum energy is described as a virtual energy potential of positive and negative energy.[93]
In quantum perturbation theory, it is sometimes said that the contribution of one-loop and multi-loop Feynman diagrams to elementary particle propagators are the contribution of vacuum fluctuations, or the zero-point energy to the particle masses.
The quantum electrodynamic vacuum
The oldest and best known quantized force field is the electromagnetic field. Maxwell's equations have been superseded by quantum electrodynamics (QED). By considering the zero-point energy that arises from QED it is possible to gain a characteristic understanding of zero-point energy that arises not just through electromagnetic interactions but in all quantum field theories.
Redefining the zero of energy
In the quantum theory of the electromagnetic field, classical wave amplitudes α and α* are replaced by operators a and a† that satisfy:
[math]\displaystyle{ \left[a,a^\dagger\right] = 1 }[/math]
The classical quantity |α|2 appearing in the classical expression for the energy of a field mode is replaced in quantum theory by the photon number operator a†a. The fact that:
[math]\displaystyle{ \left[a,a^\dagger a\right] \ne 1 }[/math]
implies that quantum theory does not allow states of the radiation field for which the photon number and a field amplitude can be precisely defined, i.e., we cannot have simultaneous eigenstates for a†a and a. The reconciliation of wave and particle attributes of the field is accomplished via the association of a probability amplitude with a classical mode pattern. The calculation of field modes is entirely classical problem, while the quantum properties of the field are carried by the mode "amplitudes" a† and a associated with these classical modes.
The zero-point energy of the field arises formally from the non-commutativity of a and a†. This is true for any harmonic oscillator: the zero-point energy ħω/2 appears when we write the Hamiltonian:
[math]\displaystyle{ \begin{align} H_{cl} &= \frac{p^2}{2m} + \tfrac{1}{2} m \omega^2 {q}^2 \\ &= \tfrac{1}{2} \hbar \omega \left(a a^\dagger + a^\dagger a\right) \\ &=\hbar \omega \left(a^\dagger a +\tfrac{1}{2}\right) \end{align} }[/math]
It is often argued that the entire universe is completely bathed in the zero-point electromagnetic field, and as such it can add only some constant amount to expectation values. Physical measurements will therefore reveal only deviations from the vacuum state. Thus the zero-point energy can be dropped from the Hamiltonian by redefining the zero of energy, or by arguing that it is a constant and therefore has no effect on Heisenberg equations of motion. Thus we can choose to declare by fiat that the ground state has zero energy and a field Hamiltonian, for example, can be replaced by:[10]
[math]\displaystyle{ \begin{align} H_F - \left\langle 0|H_F|0\right\rangle &=\tfrac{1}{2} \hbar \omega \left(a a^\dagger + a^\dagger a\right)-\tfrac{1}{2}\hbar \omega \\ &= \hbar \omega \left(a^\dagger a + \tfrac{1}{2} \right)-\tfrac{1}{2}\hbar \omega \\ &= \hbar \omega a^\dagger a \end{align} }[/math]
without affecting any physical predictions of the theory. The new Hamiltonian is said to be normally ordered (or Wick ordered) and is denoted by a double-dot symbol. The normally ordered Hamiltonian is denoted :HF, i.e.:
[math]\displaystyle{ :H_F : \equiv \hbar \omega \left(a a^\dagger + a^\dagger a\right) : \equiv \hbar \omega a^\dagger a }[/math]
In other words, within the normal ordering symbol we can commute a and a†. Since zero-point energy is intimately connected to the non-commutativity of a and a†, the normal ordering procedure eliminates any contribution from the zero-point field. This is especially reasonable in the case of the field Hamiltonian, since the zero-point term merely adds a constant energy which can be eliminated by a simple redefinition for the zero of energy. Moreover, this constant energy in the Hamiltonian obviously commutes with a and a† and so cannot have any effect on the quantum dynamics described by the Heisenberg equations of motion.
However, things are not quite that simple. The zero-point energy cannot be eliminated by dropping its energy from the Hamiltonian: When we do this and solve the Heisenberg equation for a field operator, we must include the vacuum field, which is the homogeneous part of the solution for the field operator. In fact we can show that the vacuum field is essential for the preservation of the commutators and the formal consistency of QED. When we calculate the field energy we obtain not only a contribution from particles and forces that may be present but also a contribution from the vacuum field itself i.e. the zero-point field energy. In other words, the zero-point energy reappears even though we may have deleted it from the Hamiltonian.[94]
The electromagnetic field in free space
From Maxwell's equations, the electromagnetic energy of a "free" field i.e. one with no sources, is described by:
[math]\displaystyle{ \begin{align} H_F &= \frac{1}{8\pi}\int d^3r \left(\mathbf{E}^2 +\mathbf{B}^2\right) \\ &=\frac{k^2}{2\pi}|\alpha (t)|^2 \end{align} }[/math]
We introduce the "mode function" A0(r) that satisfies the Helmholtz equation:
[math]\displaystyle{ \left( \nabla^2 + k^2 \right) \mathbf{A}_0(\mathbf{r}) = 0 }[/math]
where k = ω/c and assume it is normalized such that:
[math]\displaystyle{ \int d^3r \left|\mathbf{A}_0(\mathbf{r})\right|^2 = 1 }[/math]
We wish to "quantize" the electromagnetic energy of free space for a multimode field. The field intensity of free space should be independent of position such that |A0(r)|2 should be independent of r for each mode of the field. The mode function satisfying these conditions is:
[math]\displaystyle{ \mathbf{A}_0(\mathbf{r}) = e_{\mathbf{k}}e^{i\mathbf{k}\cdot\mathbf{r}} }[/math]
where k · ek = 0 in order to have the transversality condition ∇ · A(r,t) satisfied for the Coulomb gauge in which we are working.
To achieve the desired normalization we pretend space is divided into cubes of volume V = L3 and impose on the field the periodic boundary condition:
[math]\displaystyle{ \mathbf{A}(x+L,y+L,z+L,t)=\mathbf{A}(x,y,z,t) }[/math]
or equivalently
[math]\displaystyle{ \left(k_x,k_y,k_z\right)=\frac{2\pi}{L}\left(n_x,n_y,n_z\right) }[/math]
where n can assume any integer value. This allows us to consider the field in any one of the imaginary cubes and to define the mode function:
[math]\displaystyle{ \mathbf{A}_\mathbf{k}(\mathbf{r})= \frac{1}\sqrt{V} e_{\mathbf{k}}e^{i\mathbf{k}\cdot\mathbf{r}} }[/math]
which satisfies the Helmholtz equation, transversality, and the "box normalization":
[math]\displaystyle{ \int_V d^3r \left|\mathbf{A}_\mathbf{k}(\mathbf{r})\right|^2 = 1 }[/math]
where ek is chosen to be a unit vector which specifies the polarization of the field mode. The condition k · ek = 0 means that there are two independent choices of ek, which we call ek1 and ek2 where ek1 · ek2 = 0 and e2k1 = e2k2 = 1. Thus we define the mode functions:
[math]\displaystyle{ \mathbf{A}_{\mathbf{k}\lambda}(\mathbf{r})=\frac{1}\sqrt{V}e_{\mathbf{k}\lambda}e^{i\mathbf{k}\cdot\mathbf{r}} \, , \quad \lambda = \begin{cases} 1\\2 \end{cases} }[/math]
in terms of which the vector potential becomes[clarification needed]:
[math]\displaystyle{ \mathbf{A}_{\mathbf{k}\lambda}(\mathbf{r},t)=\sqrt{\frac{2\pi\hbar c^2}{\omega_k V}}\left[a_{\mathbf{k}\lambda}(0)e^{i\mathbf{k}\cdot\mathbf{r}}+a_{\mathbf{k}\lambda}^\dagger(0)e^{-i\mathbf{k}\cdot\mathbf{r}}\right]e_{\mathbf{k}\lambda} }[/math]
or:
[math]\displaystyle{ \mathbf{A}_{\mathbf{k}\lambda}(\mathbf{r},t)=\sqrt{\frac{2\pi\hbar c^2}{\omega_k V}}\left[a_{\mathbf{k}\lambda}(0)e^{-i(\omega_k t-\mathbf{k}\cdot\mathbf{r})}+a_{\mathbf{k}\lambda}^\dagger(0)e^{i(\omega_k t-\mathbf{k}\cdot\mathbf{r})}\right] }[/math]
where ωk = kc and akλ, a†kλ are photon annihilation and creation operators for the mode with wave vector k and polarization λ. This gives the vector potential for a plane wave mode of the field. The condition for (kx, ky, kz) shows that there are infinitely many such modes. The linearity of Maxwell's equations allows us to write:
[math]\displaystyle{ \mathbf{A}(\mathbf{r}t)=\sum_{\mathbf{k}\lambda}\sqrt{\frac{2\pi\hbar c^2}{\omega_k V}}\left[a_{\mathbf{k}\lambda}(0)e^{i\mathbf{k}\cdot\mathbf{r}}+a_{\mathbf{k}\lambda}^\dagger(0)e^{-i\mathbf{k}\cdot\mathbf{r}}\right]e_{\mathbf{k}\lambda} }[/math]
for the total vector potential in free space. Using the fact that:
[math]\displaystyle{ \int_V d^3r \mathbf{A}_{\mathbf{k}\lambda}(\mathbf{r})\cdot \mathbf{A}_{\mathbf{k}'\lambda'}^\ast(\mathbf{r})=\delta_{\mathbf{k},\mathbf{k}'}^3\delta_{\lambda,\lambda'} }[/math]
we find the field Hamiltonian is:
[math]\displaystyle{ H_F=\sum_{\mathbf{k}\lambda}\hbar\omega_k\left(a_{\mathbf{k}\lambda}^\dagger a_{\mathbf{k}\lambda} + \tfrac{1}{2} \right) }[/math]
This is the Hamiltonian for an infinite number of uncoupled harmonic oscillators. Thus different modes of the field are independent and satisfy the commutation relations:
[math]\displaystyle{ \begin{align} \left[a_{\mathbf{k}\lambda}(t),a_{\mathbf{k}'\lambda'}^\dagger(t)\right]&=\delta_{\mathbf{k},\mathbf{k}'}^3\delta_{\lambda,\lambda'} \\[10px] \left[a_{\mathbf{k}\lambda}(t),a_{\mathbf{k}'\lambda'}(t)\right]&=\left[a_{\mathbf{k}\lambda}^\dagger(t),a_{\mathbf{k}'\lambda'}^\dagger(t)\right]=0 \end{align} }[/math]
Clearly the least eigenvalue for HF is:
[math]\displaystyle{ \sum_{\mathbf{k}\lambda}\tfrac{1}{2}\hbar\omega_k }[/math]
This state describes the zero-point energy of the vacuum. It appears that this sum is divergent – in fact highly divergent, as putting in the density factor
[math]\displaystyle{ \frac{8\pi v^2 dv}{c^3}V }[/math]
shows. The summation becomes approximately the integral:
[math]\displaystyle{ \frac{4\pi h V}{c^3}\int v^3 \, dv }[/math]
for high values of v. It diverges proportional to v4 for large v.
There are two separate questions to consider. First, is the divergence a real one such that the zero-point energy really is infinite? If we consider the volume V is contained by perfectly conducting walls, very high frequencies can only be contained by taking more and more perfect conduction. No actual method of containing the high frequencies is possible. Such modes will not be stationary in our box and thus not countable in the stationary energy content. So from this physical point of view the above sum should only extend to those frequencies which are countable; a cut-off energy is thus eminently reasonable. However, on the scale of a "universe" questions of general relativity must be included. Suppose even the boxes could be reproduced, fit together and closed nicely by curving spacetime. Then exact conditions for running waves may be possible. However the very high frequency quanta will still not be contained. As per John Wheeler's "geons"[95] these will leak out of the system. So again a cut-off is permissible, almost necessary. The question here becomes one of consistency since the very high energy quanta will act as a mass source and start curving the geometry.
This leads to the second question. Divergent or not, finite or infinite, is the zero-point energy of any physical significance? The ignoring of the whole zero-point energy is often encouraged for all practical calculations. The reason for this is that energies are not typically defined by an arbitrary data point, but rather changes in data points, so adding or subtracting a constant (even if infinite) should be allowed. However this is not the whole story, in reality energy is not so arbitrarily defined: in general relativity the seat of the curvature of spacetime is the energy content and there the absolute amount of energy has real physical meaning. There is no such thing as an arbitrary additive constant with density of field energy. Energy density curves space, and an increase in energy density produces an increase of curvature. Furthermore, the zero-point energy density has other physical consequences e.g. the Casimir effect, contribution to the Lamb shift, or anomalous magnetic moment of the electron, it is clear it is not just a mathematical constant or artifact that can be cancelled out.[96]
Necessity of the vacuum field in QED
The vacuum state of the "free" electromagnetic field (that with no sources) is defined as the ground state in which nkλ = 0 for all modes (k, λ). The vacuum state, like all stationary states of the field, is an eigenstate of the Hamiltonian but not the electric and magnetic field operators. In the vacuum state, therefore, the electric and magnetic fields do not have definite values. We can imagine them to be fluctuating about their mean value of zero.
In a process in which a photon is annihilated (absorbed), we can think of the photon as making a transition into the vacuum state. Similarly, when a photon is created (emitted), it is occasionally useful to imagine that the photon has made a transition out of the vacuum state.[54] An atom, for instance, can be considered to be "dressed" by emission and reabsorption of "virtual photons" from the vacuum. The vacuum state energy described by Σkλ ħωk/2 is infinite. We can make the replacement:
[math]\displaystyle{ \sum_{\mathbf{k}\lambda}\longrightarrow\sum_{\lambda}\left (\frac{1}{2\pi} \right )^3 \int d^3 k = \frac{V}{8\pi^3} \sum_\lambda \int d^3 k }[/math]
the zero-point energy density is:
[math]\displaystyle{ \begin{align} \frac{1}{V}\sum_{\mathbf{k}\lambda}\tfrac{1}{2}\hbar\omega_k &=\frac{2}{8\pi^3}\int d^3 k \tfrac{1}{2}\hbar\omega_k \\ &= \frac{4\pi}{4\pi^3} \int dk\,k^2 \left(\tfrac{1}{2}\hbar\omega_k\right) \\ &=\frac{\hbar}{2\pi^2 c^3} \int d\omega\,\omega^3 \end{align} }[/math]
or in other words the spectral energy density of the vacuum field:
[math]\displaystyle{ \rho_0(\omega)=\frac{\hbar\omega^3}{2\pi^2c^3} }[/math]
The zero-point energy density in the frequency range from ω1 to ω2 is therefore:
[math]\displaystyle{ \int_{\omega_1}^{\omega_2} d\omega\rho_0(\omega) = \frac{\hbar}{8\pi^2c^3}\left(\omega_2^4-\omega_1^4\right) }[/math]
This can be large even in relatively narrow "low frequency" regions of the spectrum. In the optical region from 400 to 700 nm, for instance, the above equation yields around 220 erg/cm3.
We showed in the above section that the zero-point energy can be eliminated from the Hamiltonian by the normal ordering prescription. However, this elimination does not mean that the vacuum field has been rendered unimportant or without physical consequences. To illustrate this point we consider a linear dipole oscillator in the vacuum. The Hamiltonian for the oscillator plus the field with which it interacts is:
[math]\displaystyle{ H=\frac{1}{2m}\left(\mathbf{p}-\frac{e}{c}\mathbf{A}\right)^2 + \tfrac{1}{2}m\omega_0^2\mathbf{x}^2 + H_F }[/math]
This has the same form as the corresponding classical Hamiltonian and the Heisenberg equations of motion for the oscillator and the field are formally the same as their classical counterparts. For instance the Heisenberg equations for the coordinate x and the canonical momentum p = mẋ +eA/c of the oscillator are:
[math]\displaystyle{ \begin{align} \mathbf{\dot{x}}&=(i\hbar)^{-1}[\mathbf{x}.H] = \frac{1}{m}\left(\mathbf{p}-\frac{e}{c}\mathbf{A}\right) \\ \mathbf{\dot{p}}&=(i\hbar)^{-1}[\mathbf{p}.H] \begin{align}&=\tfrac{1}{2}\nabla\left(\mathbf{p}-\frac{e}{c}\mathbf{A}\right)^2-m\omega_0^2\mathbf{\dot{x}} \\ &=-\frac{1}{m} \left[\left(\mathbf{p}-\frac{e}{c}\mathbf{A}\right) \cdot \nabla\right] \left[-\frac{e}{c}\mathbf{A}\right] - \frac{1}{m} \left(\mathbf{p}-\frac{e}{c}\mathbf{A}\right) \times \nabla \times \left[-\frac{e}{c}\mathbf{A}\right] -m\omega_0^2 \mathbf{\dot{x}} \\ &= \frac{e}{c}(\mathbf{\dot{x}}\cdot\nabla)\mathbf{A} + \frac{e}{c}\mathbf{\dot{x}} \times \mathbf{B} -m\omega_0^2 \mathbf{\dot{x}} \end{align}\end{align} }[/math]
or:
[math]\displaystyle{ \begin{align} m \mathbf{\ddot{x}} &= \mathbf{\dot{p}} - \frac{e}{c} \mathbf{\dot{A}} \\ &= -\frac{e}{c} \left[\mathbf{\dot{A}} - \left(\mathbf{\dot{x}} \cdot \nabla\right) \mathbf{A}\right] + \frac{e}{c} \mathbf{\dot{x}} \times \mathbf{B} - m\omega_0^2\mathbf{x} \\ &= e\mathbf{E} + \frac{e}{c} \mathbf{\dot{x}} \times \mathbf{B} - m\omega_0^2\mathbf{x} \end{align} }[/math]
since the rate of change of the vector potential in the frame of the moving charge is given by the convective derivative
[math]\displaystyle{ \mathbf{\dot{A}}=\frac{\partial\mathbf{A}}{\partial t} + (\mathbf{\dot{x}} \cdot \nabla) \mathbf{A}^3 \,. }[/math]
For nonrelativistic motion we may neglect the magnetic force and replace the expression for mẍ by:
[math]\displaystyle{ \begin{align} \mathbf{\ddot{x}}+\omega_0^2\mathbf{x} &\approx \frac{e}{m}\mathbf{E} \\ &\approx \sum_{\mathbf{k}\lambda} \sqrt{\frac{2\pi\hbar\omega_k}{V}} \left[a_{\mathbf{k}\lambda}(t) + a_{\mathbf{k}\lambda}^\dagger(t)\right] e_{\mathbf{k}\lambda} \end{align} }[/math]
Above we have made the electric dipole approximation in which the spatial dependence of the field is neglected. The Heisenberg equation for akλ is found similarly from the Hamiltonian to be:
[math]\displaystyle{ \dot{a}_{\mathbf{k}\lambda} = i \omega_k a_{\mathbf{k}\lambda} + ie \sqrt\frac{2\pi}{\hbar \omega_k V} \mathbf{\dot{x}} \cdot e_{\mathbf{k}\lambda} }[/math]
In the electric dipole approximation.
In deriving these equations for x, p, and akλ we have used the fact that equal-time particle and field operators commute. This follows from the assumption that particle and field operators commute at some time (say, t = 0) when the matter-field interpretation is presumed to begin, together with the fact that a Heisenberg-picture operator A(t) evolves in time as A(t) = U†(t)A(0)U(t), where U(t) is the time evolution operator satisfying
[math]\displaystyle{ i\hbar\dot{U} = HU \,,\quad U^\dagger(t) = U^{-1}(t) \,,\quad U(0) = 1 \,. }[/math]
Alternatively, we can argue that these operators must commute if we are to obtain the correct equations of motion from the Hamiltonian, just as the corresponding Poisson brackets in classical theory must vanish in order to generate the correct Hamilton equations. The formal solution of the field equation is:
[math]\displaystyle{ a_{\mathbf{k}\lambda}(t)=a_{\mathbf{k}\lambda}(0)e^{-i\omega_{k}t}+ie \sqrt{\frac{2\pi}{\hbar \omega_k V}} \int^t_0dt'\,e_{\mathbf{k}\lambda}\cdot\mathbf{\dot{x}}(t')e^{i\omega_k\left(t'-t\right)} }[/math]
and therefore the equation for ȧkλ may be written:
[math]\displaystyle{ \mathbf{\ddot{x}}+\omega^2_0\mathbf{x}=\frac{e}{m}\mathbf{E}_0(t)+\frac{e}{m}\mathbf{E}_{RR}(t) }[/math]
where:
[math]\displaystyle{ \mathbf{E}_0(t)=i\sum_{\mathbf{k}\lambda} \sqrt{\frac{2\pi\hbar \omega_k}{V}}\left[a_{\mathbf{k}\lambda}(0)e^{-i\omega_kt}-a^\dagger_{\mathbf{k}\lambda}(0)e^{i\omega_kt}\right]e_{\mathbf{k}\lambda} }[/math]
and:
[math]\displaystyle{ \mathbf{E}_{RR}(t)=-\frac{4\pi e}{V} \sum_{\mathbf{k}\lambda} \int^t_0dt'\left[e_{\mathbf{k}\lambda}\cdot\mathbf{\dot{x}}\left(t'\right)\right]\cos\omega_k\left(t'-t\right) }[/math]
It can be shown that in the radiation reaction field, if the mass m is regarded as the "observed" mass then we can take:
[math]\displaystyle{ \mathbf{E}_{RR}(t)=\frac{2e}{3c^3}\mathbf{\ddot{x}} }[/math]
The total field acting on the dipole has two parts, E0(t) and ERR(t). E0(t) is the free or zero-point field acting on the dipole. It is the homogeneous solution of the Maxwell equation for the field acting on the dipole, i.e., the solution, at the position of the dipole, of the wave equation
[math]\displaystyle{ \left[\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right]\mathbf{E}=0 }[/math]
satisfied by the field in the (source free) vacuum. For this reason E0(t) is often referred to as the "vacuum field", although it is of course a Heisenberg-picture operator acting on whatever state of the field happens to be appropriate at t = 0. ERR(t) is the source field, the field generated by the dipole and acting on the dipole.
Using the above equation for ERR(t) we obtain an equation for the Heisenberg-picture operator [math]\displaystyle{ \mathbf{x}(t) }[/math] that is formally the same as the classical equation for a linear dipole oscillator:
[math]\displaystyle{ \mathbf{\ddot{x}} + \omega^2_0\mathbf{x}-\tau \mathbf{\overset{...}{x}}=\frac{e}{m}\mathbf{E}_0(t) }[/math]
where τ = 2e2/3mc3. in this instance we have considered a dipole in the vacuum, without any "external" field acting on it. the role of the external field in the above equation is played by the vacuum electric field acting on the dipole.
Classically, a dipole in the vacuum is not acted upon by any "external" field: if there are no sources other than the dipole itself, then the only field acting on the dipole is its own radiation reaction field. In quantum theory however there is always an "external" field, namely the source-free or vacuum field E0(t).
According to our earlier equation for akλ(t) the free field is the only field in existence at t = 0 as the time at which the interaction between the dipole and the field is "switched on". The state vector of the dipole-field system at t = 0 is therefore of the form
[math]\displaystyle{ |\Psi\rangle=|\text{vac}\rangle|\psi_D\rangle \,, }[/math]
where |vac⟩ is the vacuum state of the field and |ψD⟩ is the initial state of the dipole oscillator. The expectation value of the free field is therefore at all times equal to zero:
[math]\displaystyle{ \langle\mathbf{E}_0(t)\rangle=\langle\Psi|\mathbf{E}_0(t)|\Psi\rangle=0 }[/math]
since akλ(0)|vac⟩ = 0. however, the energy density associated with the free field is infinite:
[math]\displaystyle{ \begin{align} \frac{1}{4\pi} \left\langle \mathbf{E}^2_0(t) \right\rangle &= \frac{1}{4\pi} \sum_{\mathbf{k}\lambda} \sum_{\mathbf{k'}\lambda'} \sqrt{\frac{2\pi\hbar \omega_k}{V}} \sqrt{\frac{2\pi\hbar \omega_{k'}}{V}} \times \left\langle a_{\mathbf{k}\lambda}(0)a^\dagger_{\mathbf{k'}\lambda'}(0)\right\rangle \\ &= \frac{1}{4\pi}\sum_{\mathbf{k}\lambda}\left (\frac{2\pi\hbar \omega_k}{V} \right )\\ &= \int^\infin_0dw\,\rho_0(\omega) \end{align} }[/math]
The important point of this is that the zero-point field energy HF does not affect the Heisenberg equation for akλ since it is a c-number or constant (i.e. an ordinary number rather than an operator) and commutes with akλ. We can therefore drop the zero-point field energy from the Hamiltonian, as is usually done. But the zero-point field re-emerges as the homogeneous solution for the field equation. A charged particle in the vacuum will therefore always see a zero-point field of infinite density. This is the origin of one of the infinities of quantum electrodynamics, and it cannot be eliminated by the trivial expedient dropping of the term Σkλ ħωk/2 in the field Hamiltonian.
The free field is in fact necessary for the formal consistency of the theory. In particular, it is necessary for the preservation of the commutation relations, which is required by the unitary of time evolution in quantum theory:
[math]\displaystyle{ \begin{align} \left[z(t),p_z(t)\right]&=\left[U^\dagger(t)z(0)U(t),U^\dagger(t)p_z(0)U(t)\right]\\ &=U^\dagger(t)\left[z(0),p_z(0)\right]U(t)\\ &=i\hbar U^\dagger(t)U(t)\\ &=i\hbar \end{align} }[/math]
We can calculate [z(t),pz(t)] from the formal solution of the operator equation of motion
[math]\displaystyle{ \mathbf{\ddot{x}} + \omega^2_0\mathbf{x}-\tau \mathbf{\overset{...}{x}}=\frac{e}{m}\mathbf{E}_0(t) }[/math]
Using the fact that
[math]\displaystyle{ \left[a_{\mathbf{k}\lambda}(0),a^\dagger_{\mathbf{k'}\lambda'}(0)\right]=\delta^3_\mathbf{kk'},\delta_{\lambda\lambda'} }[/math]
and that equal-time particle and field operators commute, we obtain:
[math]\displaystyle{ \begin{align} [z(t),p_z(t)]&=\left[z(t),m\dot{z}(t)\right]+\left[z(t),\frac{e}{c}A_z(t)\right] \\ &=\left[z(t),m\dot{z}(t)\right] \\ &= \left (\frac{i\hbar e^2}{2\pi^2mc^3} \right ) \left (\frac{8\pi}{3} \right ) \int^\infin_0\frac{d\omega\,\omega^4}{\left(\omega^2-\omega^2_0\right)^2+\tau^2\omega^6} \end{align} }[/math]
For the dipole oscillator under consideration it can be assumed that the radiative damping rate is small compared with the natural oscillation frequency, i.e., τω0 ≪ 1. Then the integrand above is sharply peaked at ω = ω0 and:
[math]\displaystyle{ \begin{align} \left[z(t),p_z(t)\right]&\approx \frac{2i\hbar e^2}{3\pi mc^3}\omega^3_0 \int^\infin_{-\infin} \frac{dx}{x^2 + \tau^2\omega^6_0} \\ &= \left (\frac{2i\hbar e^2 \omega^3_0}{3\pi mc^3} \right )\left (\frac{\pi}{\tau\omega^3_0} \right ) \\ &=i\hbar \end{align} }[/math]
the necessity of the vacuum field can also be appreciated by making the small damping approximation in
[math]\displaystyle{ \begin{align} &\mathbf{\ddot{x}} + \omega^2_0\mathbf{x}-\tau \mathbf{\overset{...}{x}}=\frac{e}{m}\mathbf{E}_0(t) \\ &\mathbf{\ddot{x}}\approx-\omega^2_0\mathbf{x}(t) && \mathbf{\overset{...}{x}}\approx-\omega^2_0\mathbf{\dot{x}} \end{align} }[/math]
and
[math]\displaystyle{ \mathbf{\ddot{x}}+\tau\omega^2_0\mathbf{\dot{x}}+\omega^2_0\mathbf{x}\approx\frac{e}{m}\mathbf{E}_0(t) }[/math]
Without the free field E0(t) in this equation the operator x(t) would be exponentially dampened, and commutators like [z(t),pz(t)] would approach zero for t ≫ 1/τω20. With the vacuum field included, however, the commutator is iħ at all times, as required by unitarity, and as we have just shown. A similar result is easily worked out for the case of a free particle instead of a dipole oscillator.[97]
What we have here is an example of a "fluctuation-dissipation elation". Generally speaking if a system is coupled to a bath that can take energy from the system in an effectively irreversible way, then the bath must also cause fluctuations. The fluctuations and the dissipation go hand in hand we cannot have one without the other. In the current example the coupling of a dipole oscillator to the electromagnetic field has a dissipative component, in the form of the zero-point (vacuum) field; given the existence of radiation reaction, the vacuum field must also exist in order to preserve the canonical commutation rule and all it entails.
The spectral density of the vacuum field is fixed by the form of the radiation reaction field, or vice versa: because the radiation reaction field varies with the third derivative of x, the spectral energy density of the vacuum field must be proportional to the third power of ω in order for [z(t),pz(t)] to hold. In the case of a dissipative force proportional to ẋ, by contrast, the fluctuation force must be proportional to [math]\displaystyle{ \omega }[/math] in order to maintain the canonical commutation relation.[97] This relation between the form of the dissipation and the spectral density of the fluctuation is the essence of the fluctuation-dissipation theorem.[76]
The fact that the canonical commutation relation for a harmonic oscillator coupled to the vacuum field is preserved implies that the zero-point energy of the oscillator is preserved. it is easy to show that after a few damping times the zero-point motion of the oscillator is in fact sustained by the driving zero-point field.[98]
The quantum chromodynamic vacuum
The QCD vacuum is the vacuum state of quantum chromodynamics (QCD). It is an example of a non-perturbative vacuum state, characterized by a non-vanishing condensates such as the gluon condensate and the quark condensate in the complete theory which includes quarks. The presence of these condensates characterizes the confined phase of quark matter. In technical terms, gluons are vector gauge bosons that mediate strong interactions of quarks in quantum chromodynamics (QCD). Gluons themselves carry the color charge of the strong interaction. This is unlike the photon, which mediates the electromagnetic interaction but lacks an electric charge. Gluons therefore participate in the strong interaction in addition to mediating it, making QCD significantly harder to analyze than QED (quantum electrodynamics) as it deals with nonlinear equations to characterize such interactions.
The Higgs field
The Standard Model hypothesises a field called the Higgs field (symbol: ϕ), which has the unusual property of a non-zero amplitude in its ground state (zero-point) energy after renormalization; i.e., a non-zero vacuum expectation value. It can have this effect because of its unusual "Mexican hat" shaped potential whose lowest "point" is not at its "centre". Below a certain extremely high energy level the existence of this non-zero vacuum expectation spontaneously breaks electroweak gauge symmetry which in turn gives rise to the Higgs mechanism and triggers the acquisition of mass by those particles interacting with the field. The Higgs mechanism occurs whenever a charged field has a vacuum expectation value. This effect occurs because scalar field components of the Higgs field are "absorbed" by the massive bosons as degrees of freedom, and couple to the fermions via Yukawa coupling, thereby producing the expected mass terms. The expectation value of ϕ0 in the ground state (the vacuum expectation value or VEV) is then ⟨ϕ0⟩ = v/√2, where v = |μ|/√λ. The measured value of this parameter is approximately 246 GeV/c2.[99] It has units of mass, and is the only free parameter of the Standard Model that is not a dimensionless number.
The Higgs mechanism is a type of superconductivity which occurs in the vacuum. It occurs when all of space is filled with a sea of particles which are charged and thus the field has a nonzero vacuum expectation value. Interaction with the vacuum energy filling the space prevents certain forces from propagating over long distances (as it does in a superconducting medium; e.g., in the Ginzburg–Landau theory).
Experimental observations
Zero-point energy has many observed physical consequences.[11] It is important to note that zero-point energy is not merely an artifact of mathematical formalism that can, for instance, be dropped from a Hamiltonian by redefining the zero of energy, or by arguing that it is a constant and therefore has no effect on Heisenberg equations of motion without latter consequence.[100] Indeed, such treatment could create a problem at a deeper, as of yet undiscovered, theory.[101] For instance, in general relativity the zero of energy (i.e. the energy density of the vacuum) contributes to a cosmological constant of the type introduced by Einstein in order to obtain static solutions to his field equations.[102] The zero-point energy density of the vacuum, due to all quantum fields, is extremely large, even when we cut off the largest allowable frequencies based on plausible physical arguments. It implies a cosmological constant larger than the limits imposed by observation by about 120 orders of magnitude. This "cosmological constant problem" remains one of the greatest unsolved mysteries of physics.[103]
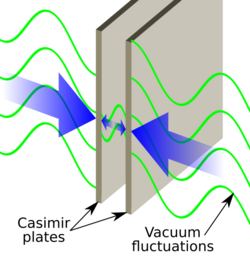
Casimir effect
A phenomenon that is commonly presented as evidence for the existence of zero-point energy in vacuum is the Casimir effect, proposed in 1948 by Dutch physicist Hendrik Casimir, who considered the quantized electromagnetic field between a pair of grounded, neutral metal plates. The vacuum energy contains contributions from all wavelengths, except those excluded by the spacing between plates. As the plates draw together, more wavelengths are excluded and the vacuum energy decreases. The decrease in energy means there must be a force doing work on the plates as they move.
Early experimental tests from the 1950s onwards gave positive results showing the force was real, but other external factors could not be ruled out as the primary cause, with the range of experimental error sometimes being nearly 100%.[104][105][106][107][108] That changed in 1997 with Lamoreaux[109] conclusively showing that the Casimir force was real. Results have been repeatedly replicated since then.[110][111][112][113]
In 2009, Munday et al.[114] published experimental proof that (as predicted in 1961[115]) the Casimir force could also be repulsive as well as being attractive. Repulsive Casimir forces could allow quantum levitation of objects in a fluid and lead to a new class of switchable nanoscale devices with ultra-low static friction.[116]
An interesting hypothetical side effect of the Casimir effect is the Scharnhorst effect, a hypothetical phenomenon in which light signals travel slightly faster than c between two closely spaced conducting plates.[117]
Lamb shift
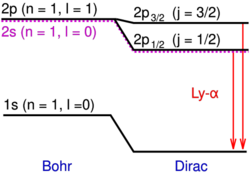
The quantum fluctuations of the electromagnetic field have important physical consequences. In addition to the Casimir effect, they also lead to a splitting between the two energy levels 2S1/2 and 2P1/2 (in term symbol notation) of the hydrogen atom which was not predicted by the Dirac equation, according to which these states should have the same energy. Charged particles can interact with the fluctuations of the quantized vacuum field, leading to slight shifts in energy;[118] this effect is called the Lamb shift.[119] The shift of about 4.38×10−6 eV is roughly 10−7 of the difference between the energies of the 1s and 2s levels, and amounts to 1,058 MHz in frequency units. A small part of this shift (27 MHz ≈ 3%) arises not from fluctuations of the electromagnetic field, but from fluctuations of the electron–positron field. The creation of (virtual) electron–positron pairs has the effect of screening the Coulomb field and acts as a vacuum dielectric constant. This effect is much more important in muonic atoms.[120]
Fine-structure constant
Taking ħ (Planck's constant divided by 2π), c (the speed of light), and e2 = q2e/4πε0 (the electromagnetic coupling constant i.e. a measure of the strength of the electromagnetic force (where qe is the absolute value of the electronic charge and [math]\displaystyle{ \varepsilon_0 }[/math] is the vacuum permittivity)) we can form a dimensionless quantity called the fine-structure constant:
[math]\displaystyle{ \alpha = \frac{e^2}{\hbar c} = \frac{q_e^2}{4\pi\varepsilon_0\hbar c} \approx \frac{1}{137} }[/math]
The fine-structure constant is the coupling constant of quantum electrodynamics (QED) determining the strength of the interaction between electrons and photons. It turns out that the fine-structure constant is not really a constant at all owing to the zero-point energy fluctuations of the electron-positron field.[121] The quantum fluctuations caused by zero-point energy have the effect of screening electric charges: owing to (virtual) electron-positron pair production, the charge of the particle measured far from the particle is far smaller than the charge measured when close to it.
The Heisenberg inequality where ħ = h/2π, and Δx, Δp are the standard deviations of position and momentum states that:
[math]\displaystyle{ \Delta_x\Delta_p\ge\frac{1}{2}\hbar }[/math]
It means that a short distance implies large momentum and therefore high energy i.e. particles of high energy must be used to explore short distances. QED concludes that the fine-structure constant is an increasing function of energy. It has been shown that at energies of the order of the Z0 boson rest energy, mzc2 ≈ 90 GeV, that:
[math]\displaystyle{ \alpha\approx\frac{1}{129} }[/math]
rather than the low-energy α ≈ 1/137.[122][123] The renormalization procedure of eliminating zero-point energy infinities allows the choice of an arbitrary energy (or distance) scale for defining α. All in all, α depends on the energy scale characteristic of the process under study, and also on details of the renormalization procedure. The energy dependence of α has been observed for several years now in precision experiment in high-energy physics.
Vacuum birefringence
File:Eso1641a.ogg In the presence of strong electrostatic fields it is predicted that virtual particles become separated from the vacuum state and form real matter.[citation needed] The fact that electromagnetic radiation can be transformed into matter and vice versa leads to fundamentally new features in quantum electrodynamics. One of the most important consequences is that, even in the vacuum, the Maxwell equations have to be exchanged by more complicated formulas. In general, it will be not possible to separate processes in the vacuum from the processes involving matter since electromagnetic fields can create matter if the field fluctuations are strong enough. This leads to highly complex nonlinear interaction - gravity will have an effect on the light at the same time the light has an effect on gravity. These effects were first predicted by Werner Heisenberg and Hans Heinrich Euler in 1936[124] and independently the same year by Victor Weisskopf who stated: "The physical properties of the vacuum originate in the "zero-point energy" of matter, which also depends on absent particles through the external field strengths and therefore contributes an additional term to the purely Maxwellian field energy".[125][126] Thus strong magnetic fields vary the energy contained in the vacuum. The scale above which the electromagnetic field is expected to become nonlinear is known as the Schwinger limit. At this point the vacuum has all the properties of a birefringent medium, thus in principle a rotation of the polarization frame (the Faraday effect) can be observed in empty space.[127][128]
Both Einstein's theory of special and general relativity state that light should pass freely through a vacuum without being altered, a principle known as Lorentz invariance. Yet, in theory, large nonlinear self-interaction of light due to quantum fluctuations should lead to this principle being measurably violated if the interactions are strong enough. Nearly all theories of quantum gravity predict that Lorentz invariance is not an exact symmetry of nature. It is predicted the speed at which light travels through the vacuum depends on its direction, polarization and the local strength of the magnetic field.[129] There have been a number of inconclusive results which claim to show evidence of a Lorentz violation by finding a rotation of the polarization plane of light coming from distant galaxies.[130] The first concrete evidence for vacuum birefringence was published in 2017 when a team of astronomers looked at the light coming from the star RX J1856.5-3754,[131] the closest discovered neutron star to Earth.[132]
Roberto Mignani at the National Institute for Astrophysics in Milan who led the team of astronomers has commented that "When Einstein came up with the theory of general relativity 100 years ago, he had no idea that it would be used for navigational systems. The consequences of this discovery probably will also have to be realised on a longer timescale."[133] The team found that visible light from the star had undergone linear polarisation[clarification needed] of around 16%. If the birefringence had been caused by light passing through interstellar gas or plasma, the effect should have been no more than 1%. Definitive proof would require repeating the observation at other wavelengths and on other neutron stars. At X-ray wavelengths the polarization from the quantum fluctuations should be near 100%.[134] Although no telescope currently exists that can make such measurements, there are several proposed X-ray telescopes that may soon be able to verify the result conclusively such as China's Hard X-ray Modulation Telescope (HXMT) and NASA's Imaging X-ray Polarimetry Explorer (IXPE).
Speculated involvement in other phenomena
Dark energy
| Unsolved problem in physics: Why does the large zero-point energy of the vacuum not cause a large cosmological constant? What cancels it out?[18][103][135] (more unsolved problems in physics)
|
In the late 1990s it was discovered that very distant supernovae were dimmer than expected suggesting that the universe's expansion was accelerating rather than slowing down.[136][137] This revived discussion that Einstein's cosmological constant, long disregarded by physicists as being equal to zero, was in fact some small positive value. This would indicate empty space exerted some form of negative pressure or energy.
There is no natural candidate for what might cause what has been called dark energy but the current best guess is that it is the zero-point energy of the vacuum.[138] One difficulty with this assumption is that the zero-point energy of the vacuum is absurdly large compared to the observed cosmological constant. This issue, called the cosmological constant problem, is one of the greatest unsolved mysteries in physics.
The European Space Agency's Euclid telescope, launched on 1 July 2023, will map galaxies up to 10 billion light years away.[139] By seeing how dark energy influences their arrangement and shape, the mission will allow scientists to see if the strength of dark energy has changed. If dark energy is found to vary throughout time it would indicate it is due to quintessence, where observed acceleration is due to the energy of a scalar field, rather than the cosmological constant. No evidence of quintessence is yet available, but it has not been ruled out either. It generally predicts a slightly slower acceleration of the expansion of the universe than the cosmological constant. Some scientists think that the best evidence for quintessence would come from violations of Einstein's equivalence principle and variation of the fundamental constants in space or time.[140] Scalar fields are predicted by the Standard Model of particle physics and string theory, but an analogous problem to the cosmological constant problem (or the problem of constructing models of cosmological inflation) occurs: renormalization theory predicts that scalar fields should acquire large masses again due to zero-point energy.
Cosmic inflation
| Unsolved problem in physics: Why does the observable universe have more matter than antimatter? (more unsolved problems in physics)
|
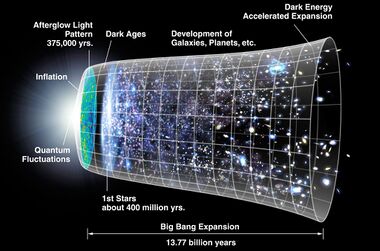
Cosmic inflation is phase of accelerated cosmic expansion just after the Big Bang. It explains the origin of the large-scale structure of the cosmos. It is believed quantum vacuum fluctuations caused by zero-point energy arising in the microscopic inflationary period, later became magnified to a cosmic size, becoming the gravitational seeds for galaxies and structure in the Universe (see galaxy formation and evolution and structure formation).[141] Many physicists also believe that inflation explains why the Universe appears to be the same in all directions (isotropic), why the cosmic microwave background radiation is distributed evenly, why the Universe is flat, and why no magnetic monopoles have been observed.
The mechanism for inflation is unclear, it is similar in effect to dark energy but is a far more energetic and short lived process. As with dark energy the best explanation is some form of vacuum energy arising from quantum fluctuations. It may be that inflation caused baryogenesis, the hypothetical physical processes that produced an asymmetry (imbalance) between baryons and antibaryons produced in the very early universe, but this is far from certain.
Alternative theories
There has been a long debate[142] over the question of whether zero-point fluctuations of quantized vacuum fields are "real" i.e. do they have physical effects that cannot be interpreted by an equally valid alternative theory? Schwinger, in particular, attempted to formulate QED without reference to zero-point fluctuations via his "source theory".[143] From such an approach it is possible to derive the Casimir Effect without reference to a fluctuating field. Such a derivation was first given by Schwinger (1975)[144] for a scalar field, and then generalized to the electromagnetic case by Schwinger, DeRaad, and Milton (1978).[145] in which they state "the vacuum is regarded as truly a state with all physical properties equal to zero". More recently Jaffe (2005)[146] has highlighted a similar approach in deriving the Casimir effect stating "the concept of zero-point fluctuations is a heuristic and calculational aid in the description of the Casimir effect, but not a necessity in QED."
Nevertheless, as Jaffe himself notes in his paper, "no one has shown that source theory or another S-matrix based approach can provide a complete description of QED to all orders." Furthermore, Milonni has shown the necessity of the vacuum field for the formal consistency of QED.[147] In QCD, color confinement has led physicists to abandon the source theory or S-matrix based approach for the strong interactions. The Higgs mechanism, Hawking Radiation and the Unruh effect are also theorized to be dependent on zero-point vacuum fluctuations, the field contribution being an inseparable parts of these theories. Jaffe continues "Even if one could argue away zero-point contributions to the quantum vacuum energy, the problem of spontaneous symmetry breaking remains: condensates [ground state vacua] that carry energy appear at many energy scales in the Standard Model. So there is good reason to be skeptical of attempts to avoid the standard formulation of quantum field theory and the zero-point energies it brings with it." It is difficult to judge the physical reality of infinite zero-point energies that are inherent in field theories, but modern physics does not know any better way to construct gauge-invariant, renormalizable theories than with zero-point energy and they would seem to be a necessity for any attempt at a unified theory.[148]
Chaotic and emergent phenomena
| Beyond the Standard Model |
|---|
 |
| Standard Model |
The mathematical models used in classical electromagnetism, quantum electrodynamics (QED) and the Standard Model all view the electromagnetic vacuum as a linear system with no overall observable consequence. For example, in the case of the Casimir effect, Lamb shift, and so on these phenomena can be explained by alternative mechanisms other than action of the vacuum by arbitrary changes to the normal ordering of field operators. See the alternative theories section. This is a consequence of viewing electromagnetism as a U(1) gauge theory, which topologically does not allow the complex interaction of a field with and on itself.[149] In higher symmetry groups and in reality, the vacuum is not a calm, randomly fluctuating, largely immaterial and passive substance, but at times can be viewed as a turbulent virtual plasma that can have complex vortices (i.e. solitons vis-à-vis particles), entangled states and a rich nonlinear structure.[150] There are many observed nonlinear physical electromagnetic phenomena such as Aharonov–Bohm (AB)[151][152] and Altshuler–Aronov–Spivak (AAS) effects,[153] Berry,[154] Aharonov–Anandan,[155] Pancharatnam[156] and Chiao–Wu[157] phase rotation effects, Josephson effect,[158][159] Quantum Hall effect,[160] the De Haas–Van Alphen effect,[161] the Sagnac effect and many other physically observable phenomena which would indicate that the electromagnetic potential field has real physical meaning rather than being a mathematical artifact[162] and therefore an all encompassing theory would not confine electromagnetism as a local force as is currently done, but as a SU(2) gauge theory or higher geometry. Higher symmetries allow for nonlinear, aperiodic behaviour which manifest as a variety of complex non-equilibrium phenomena that do not arise in the linearised U(1) theory, such as multiple stable states, symmetry breaking, chaos and emergence.[163]
What are called Maxwell's equations today, are in fact a simplified version of the original equations reformulated by Heaviside, FitzGerald, Lodge and Hertz. The original equations used Hamilton's more expressive quaternion notation,[164] a kind of Clifford algebra, which fully subsumes the standard Maxwell vectorial equations largely used today.[165] In the late 1880s there was a debate over the relative merits of vector analysis and quaternions. According to Heaviside the electromagnetic potential field was purely metaphysical, an arbitrary mathematical fiction, that needed to be "murdered".[166] It was concluded that there was no need for the greater physical insights provided by the quaternions if the theory was purely local in nature. Local vector analysis has become the dominant way of using Maxwell's equations ever since. However, this strictly vectorial approach has led to a restrictive topological understanding in some areas of electromagnetism, for example, a full understanding of the energy transfer dynamics in Tesla's oscillator-shuttle-circuit can only be achieved in quaternionic algebra or higher SU(2) symmetries.[167] It has often been argued that quaternions are not compatible with special relativity,[168] but multiple papers have shown ways of incorporating relativity.[169][170][171][172]
A good example of nonlinear electromagnetics is in high energy dense plasmas, where vortical phenomena occur which seemingly violate the second law of thermodynamics by increasing the energy gradient within the electromagnetic field and violate Maxwell's laws by creating ion currents which capture and concentrate their own and surrounding magnetic fields. In particular Lorentz force law, which elaborates Maxwell's equations is violated by these force free vortices.[173][174][175] These apparent violations are due to the fact that the traditional conservation laws in classical and quantum electrodynamics (QED) only display linear U(1) symmetry (in particular, by the extended Noether theorem,[176] conservation laws such as the laws of thermodynamics need not always apply to dissipative systems,[177][178] which are expressed in gauges of higher symmetry). The second law of thermodynamics states that in a closed linear system entropy flow can only be positive (or exactly zero at the end of a cycle). However, negative entropy (i.e. increased order, structure or self-organisation) can spontaneously appear in an open nonlinear thermodynamic system that is far from equilibrium, so long as this emergent order accelerates the overall flow of entropy in the total system. The 1977 Nobel Prize in Chemistry was awarded to thermodynamicist Ilya Prigogine[179] for his theory of dissipative systems that described this notion. Prigogine described the principle as "order through fluctuations"[180] or "order out of chaos".[181] It has been argued by some that all emergent order in the universe from galaxies, solar systems, planets, weather, complex chemistry, evolutionary biology to even consciousness, technology and civilizations are themselves examples of thermodynamic dissipative systems; nature having naturally selected these structures to accelerate entropy flow within the universe to an ever-increasing degree.[182] For example, it has been estimated that human body is 10,000 times more effective at dissipating energy per unit of mass than the sun.[183]
One may query what this has to do with zero-point energy. Given the complex and adaptive behaviour that arises from nonlinear systems considerable attention in recent years has gone into studying a new class of phase transitions which occur at absolute zero temperature. These are quantum phase transitions which are driven by EM field fluctuations as a consequence of zero-point energy.[184] A good example of a spontaneous phase transition that are attributed to zero-point fluctuations can be found in superconductors. Superconductivity is one of the best known empirically quantified macroscopic electromagnetic phenomena whose basis is recognised to be quantum mechanical in origin. The behaviour of the electric and magnetic fields under superconductivity is governed by the London equations. However, it has been questioned in a series of journal articles whether the quantum mechanically canonised London equations can be given a purely classical derivation.[185] Bostick,[186][187] for instance, has claimed to show that the London equations do indeed have a classical origin that applies to superconductors and to some collisionless plasmas as well. In particular it has been asserted that the Beltrami vortices in the plasma focus display the same paired flux-tube morphology as Type II superconductors.[188][189] Others have also pointed out this connection, Fröhlich[190] has shown that the hydrodynamic equations of compressible fluids, together with the London equations, lead to a macroscopic parameter ([math]\displaystyle{ \mu }[/math] = electric charge density / mass density), without involving either quantum phase factors or Planck's constant. In essence, it has been asserted that Beltrami plasma vortex structures are able to at least simulate the morphology of Type I and Type II superconductors. This occurs because the "organised" dissipative energy of the vortex configuration comprising the ions and electrons far exceeds the "disorganised" dissipative random thermal energy. The transition from disorganised fluctuations to organised helical structures is a phase transition involving a change in the condensate's energy (i.e. the ground state or zero-point energy) but without any associated rise in temperature.[191] This is an example of zero-point energy having multiple stable states (see Quantum phase transition, Quantum critical point, Topological degeneracy, Topological order[192]) and where the overall system structure is independent of a reductionist or deterministic view, that "classical" macroscopic order can also causally affect quantum phenomena. Furthermore, the pair production of Beltrami vortices has been compared to the morphology of pair production of virtual particles in the vacuum.
The idea that the vacuum energy can have multiple stable energy states is a leading hypothesis for the cause of cosmic inflation. In fact, it has been argued that these early vacuum fluctuations led to the expansion of the universe and in turn have guaranteed the non-equilibrium conditions necessary to drive order from chaos, as without such expansion the universe would have reached thermal equilibrium and no complexity could have existed. With the continued accelerated expansion of the universe, the cosmos generates an energy gradient that increases the "free energy" (i.e. the available, usable or potential energy for useful work) which the universe is able to use to create ever more complex forms of order.[193][194] The only reason Earth's environment does not decay into an equilibrium state is that it receives a daily dose of sunshine and that, in turn, is due to the sun "polluting" interstellar space with entropy. The sun's fusion power is only possible due to the gravitational disequilibrium of matter that arose from cosmic expansion. In this essence, the vacuum energy can be viewed as the key cause of the structure throughout the universe. That humanity might alter the morphology of the vacuum energy to create an energy gradient for useful work is the subject of much controversy.
Purported applications
Physicists overwhelmingly reject any possibility that the zero-point energy field can be exploited to obtain useful energy (work) or uncompensated momentum; such efforts are seen as tantamount to perpetual motion machines.
Nevertheless, the allure of free energy has motivated such research, usually falling in the category of fringe science. As long ago as 1889 (before quantum theory or discovery of the zero point energy) Nikola Tesla proposed that useful energy could be obtained from free space, or what was assumed at that time to be an all-pervasive aether.[195] Others have since claimed to exploit zero-point or vacuum energy with a large amount of pseudoscientific literature causing ridicule around the subject.[196][197] Despite rejection by the scientific community, harnessing zero-point energy remains an interest of research, particularly in the US where it has attracted the attention of major aerospace/defence contractors and the U.S. Department of Defense as well as in China, Germany, Russia and Brazil.[196][198]
Casimir batteries and engines
A common assumption is that the Casimir force is of little practical use; the argument is made that the only way to actually gain energy from the two plates is to allow them to come together (getting them apart again would then require more energy), and therefore it is a one-use-only tiny force in nature.[196] In 1984 Robert Forward[199] published work showing how a "vacuum-fluctuation battery" could be constructed. The battery can be recharged by making the electrical forces slightly stronger than the Casimir force to reexpand the plates.[citation needed]
In 1995 and 1998 Maclay et al.[200][201] published the first models of a microelectromechanical system (MEMS) with Casimir forces. While not exploiting the Casimir force for useful work, the papers drew attention from the MEMS community due to the revelation that Casimir effect needs to be considered as a vital factor in the future design of MEMS. In particular, Casimir effect might be the critical factor in the stiction failure of MEMS.[202]
In 1999, Pinto, a former scientist at NASA's Jet Propulsion Laboratory at Caltech in Pasadena, published in Physical Review his thought experiment (Gedankenexperiment) for a "Casimir engine". The paper showed that continuous positive net exchange of energy from the Casimir effect was possible, even stating in the abstract "In the event of no other alternative explanations, one should conclude that major technological advances in the area of endless, by-product free-energy production could be achieved."[203]
In 2001, Capasso et al. showed how the force can be used to control the mechanical motion of a MEMS device, The researchers suspended a polysilicon plate from a torsional rod – a twisting horizontal bar just a few microns in diameter. When they brought a metallized sphere close up to the plate, the attractive Casimir force between the two objects made the plate rotate. They also studied the dynamical behaviour of the MEMS device by making the plate oscillate. The Casimir force reduced the rate of oscillation and led to nonlinear phenomena, such as hysteresis and bistability in the frequency response of the oscillator. According to the team, the system's behaviour agreed well with theoretical calculations.[111]
Despite this and several similar peer-reviewed papers, there is not a consensus as to whether such devices can produce a continuous output of work. Garret Moddel at University of Colorado has highlighted that he believes such devices hinge on the assumption that the Casimir force is a nonconservative force, he argues that there is sufficient evidence (e.g. analysis by Scandurra (2001)[204]) to say that the Casimir effect is a conservative force and therefore even though such an engine can exploit the Casimir force for useful work it cannot produce more output energy than has been input into the system.[205]
In 2008, DARPA solicited research proposals in the area of Casimir Effect Enhancement (CEE).[206] The goal of the program is to develop new methods to control and manipulate attractive and repulsive forces at surfaces based on engineering of the Casimir force.[citation needed]
A 2008 patent by Haisch and Moddel[207] details a device that is able to extract power from zero-point fluctuations using a gas that circulates through a Casimir cavity. As gas atoms circulate around the system they enter the cavity. Upon entering the electrons spin down to release energy via electromagnetic radiation. This radiation is then extracted by an absorber. On exiting the cavity the ambient vacuum fluctuations (i.e. the zero-point field) impart energy on the electrons to return the orbitals to previous energy levels, as predicted by Senitzky (1960).[98] The gas then goes through a pump and flows through the system again. A published test of this concept by Moddel[208] was performed in 2012 and seemed to give excess energy that could not be attributed to another source. However it has not been conclusively shown to be from zero-point energy and the theory requires further investigation.[209]
Single heat baths
In 1951 Callen and Welton[76] proved the quantum fluctuation-dissipation theorem (FDT) which was originally formulated in classical form by Nyquist (1928)[77] as an explanation for observed Johnson noise[78] in electric circuits. Fluctuation-dissipation theorem showed that when something dissipates energy, in an effectively irreversible way, a connected heat bath must also fluctuate. The fluctuations and the dissipation go hand in hand; it is impossible to have one without the other. The implication of FDT being that the vacuum could be treated as a heat bath coupled to a dissipative force and as such energy could, in part, be extracted from the vacuum for potentially useful work.[79] Such a theory has met with resistance: Macdonald (1962)[210] and Harris (1971)[211] claimed that extracting power from the zero-point energy to be impossible, so FDT could not be true. Grau and Kleen (1982)[212] and Kleen (1986),[213] argued that the Johnson noise of a resistor connected to an antenna must satisfy Planck's thermal radiation formula, thus the noise must be zero at zero temperature and FDT must be invalid. Kiss (1988)[214] pointed out that the existence of the zero-point term may indicate that there is a renormalization problem—i.e., a mathematical artifact—producing an unphysical term that is not actually present in measurements (in analogy with renormalization problems of ground states in quantum electrodynamics). Later, Abbott et al. (1996) arrived at a different but unclear conclusion that "zero-point energy is infinite thus it should be renormalized but not the 'zero-point fluctuations'".[215] Despite such criticism, FDT has been shown to be true experimentally under certain quantum, non-classical conditions. Zero-point fluctuations can, and do, contribute towards systems which dissipate energy.[80] A paper by Armen Allahverdyan and Theo Nieuwenhuizen in 2000 showed the feasibility of extracting zero-point energy for useful work from a single bath, without contradicting the laws of thermodynamics, by exploiting certain quantum mechanical properties.[81]
There have been a growing number of papers showing that in some instances the classical laws of thermodynamics, such as limits on the Carnot efficiency, can be violated by exploiting negative entropy of quantum fluctuations.[82][216][217][218][219][220][221][222][223][224]
Despite efforts to reconcile quantum mechanics and thermodynamics over the years, their compatibility is still an open fundamental problem. The full extent that quantum properties can alter classical thermodynamic bounds is unknown[225]
Space travel and unconventional approaches
The use of zero-point energy for space travel is speculative and does not form part of the mainstream scientific consensus. A complete quantum theory of gravitation (that would deal with the role of quantum phenomena like zero-point energy) does not yet exist. Speculative papers explaining a relationship between zero-point energy and gravitational shielding effects have been proposed,[16][226][227][228] but the interaction (if any) is not yet fully understood. Most serious scientific research in this area depends on the theorized anti-gravitational properties of antimatter (currently being tested at the alpha experiment at CERN) and/or the effects of non-Newtonian forces such as the gravitomagnetic field under specific quantum conditions. According to the general theory of relativity, rotating matter can generate a new force of nature, known as the gravitomagnetic interaction, whose intensity is proportional to the rate of spin.[229] In certain conditions the gravitomagnetic field can be repulsive. In neutrons stars for example it can produce a gravitational analogue of the Meissner effect, but the force produced in such an example is theorized to be exceedingly weak.[230]
In 1963 Robert Forward, a physicist and aerospace engineer at Hughes Research Laboratories, published a paper showing how within the framework of general relativity "anti-gravitational" effects might be achieved.[231] Since all atoms have spin, gravitational permeability may be able to differ from material to material. A strong toroidal gravitational field that acts against the force of gravity could be generated by materials that have nonlinear properties that enhance time-varying gravitational fields. Such an effect would be analogous to the nonlinear electromagnetic permeability of iron making it an effective core (i.e. the doughnut of iron) in a transformer, whose properties are dependent on magnetic permeability.[232][233][234] In 1966 Dewitt[235] was first to identify the significance of gravitational effects in superconductors. Dewitt demonstrated that a magnetic-type gravitational field must result in the presence of fluxoid quantization. In 1983, Dewitt's work was substantially expanded by Ross.[236]
From 1971 to 1974 Henry William Wallace, a scientist at GE Aerospace was issued with three patents.[237][238][239] Wallace used Dewitt's theory to develop an experimental apparatus for generating and detecting a secondary gravitational field, which he named the kinemassic field (now better known as the gravitomagnetic field). In his three patents, Wallace describes three different methods used for detection of the gravitomagnetic field – change in the motion of a body on a pivot, detection of a transverse voltage in a semiconductor crystal, and a change in the specific heat of a crystal material having spin-aligned nuclei. There are no publicly available independent tests verifying Wallace's devices. Such an effect if any would be small.[240][241][242][243][244][245] Referring to Wallace's patents, a New Scientist article in 1980 stated "Although the Wallace patents were initially ignored as cranky, observers believe that his invention is now under serious but secret investigation by the military authorities in the USA. The military may now regret that the patents have already been granted and so are available for anyone to read."[246] A further reference to Wallace's patents occur in an electric propulsion study prepared for the Astronautics Laboratory at Edwards Air Force Base which states: "The patents are written in a very believable style which include part numbers, sources for some components, and diagrams of data. Attempts were made to contact Wallace using patent addresses and other sources but he was not located nor is there a trace of what became of his work. The concept can be somewhat justified on general relativistic grounds since rotating frames of time varying fields are expected to emit gravitational waves."[247]
In 1986 the U.S. Air Force 's then Rocket Propulsion Laboratory (RPL) at Edwards Air Force Base solicited "Non Conventional Propulsion Concepts" under a small business research and innovation program. One of the six areas of interest was "Esoteric energy sources for propulsion, including the quantum dynamic energy of vacuum space..." In the same year BAE Systems launched "Project Greenglow" to provide a "focus for research into novel propulsion systems and the means to power them".[198][248]
In 1988 Kip Thorne et al.[249] published work showing how traversable wormholes can exist in spacetime only if they are threaded by quantum fields generated by some form of exotic matter that has negative energy. In 1993 Scharnhorst and Barton[117] showed that the speed of a photon will be increased if it travels between two Casimir plates, an example of negative energy. In the most general sense, the exotic matter needed to create wormholes would share the repulsive properties of the inflationary energy, dark energy or zero-point radiation of the vacuum.[250] Building on the work of Thorne, in 1994 Miguel Alcubierre[251] proposed a method for changing the geometry of space by creating a wave that would cause the fabric of space ahead of a spacecraft to contract and the space behind it to expand (see Alcubierre drive). The ship would then ride this wave inside a region of flat space, known as a warp bubble and would not move within this bubble but instead be carried along as the region itself moves due to the actions of the drive.
In 1992 Evgeny Podkletnov[252] published a heavily debated[253][254][255][256] journal article claiming a specific type of rotating superconductor could shield gravitational force. Independently of this, from 1991 to 1993 Ning Li and Douglas Torr published a number of articles[257][258][259] about gravitational effects in superconductors. One finding they derived is the source of gravitomagnetic flux in a type II superconductor material is due to spin alignment of the lattice ions. Quoting from their third paper: "It is shown that the coherent alignment of lattice ion spins will generate a detectable gravitomagnetic field, and in the presence of a time-dependent applied magnetic vector potential field, a detectable gravitoelectric field." The claimed size of the generated force has been disputed by some[260][261] but defended by others.[262][263] In 1997 Li published a paper attempting to replicate Podkletnov's results and showed the effect was very small, if it existed at all.[264] Li is reported to have left the University of Alabama in 1999 to found the company AC Gravity LLC.[265] AC Gravity was awarded a U.S. DOD grant for $448,970 in 2001 to continue anti-gravity research. The grant period ended in 2002 but no results from this research were ever made public.[266]
In 2002 Phantom Works, Boeing's advanced research and development facility in Seattle, approached Evgeny Podkletnov directly. Phantom Works was blocked by Russian technology transfer controls. At this time Lieutenant General George Muellner, the outgoing head of the Boeing Phantom Works, confirmed that attempts by Boeing to work with Podkletnov had been blocked by Moscow, also commenting that "The physical principles – and Podkletnov's device is not the only one – appear to be valid... There is basic science there. They're not breaking the laws of physics. The issue is whether the science can be engineered into something workable"[267]
Froning and Roach (2002)[268] put forward a paper that builds on the work of Puthoff, Haisch and Alcubierre. They used fluid dynamic simulations to model the interaction of a vehicle (like that proposed by Alcubierre) with the zero-point field. Vacuum field perturbations are simulated by fluid field perturbations and the aerodynamic resistance of viscous drag exerted on the interior of the vehicle is compared to the Lorentz force exerted by the zero-point field (a Casimir-like force is exerted on the exterior by unbalanced zero-point radiation pressures). They find that the optimized negative energy required for an Alcubierre drive is where it is a saucer-shaped vehicle with toroidal electromagnetic fields. The EM fields distort the vacuum field perturbations surrounding the craft sufficiently to affect the permeability and permittivity of space.
In 2009 Giorgio Fontana and Bernd Binder presented a new method to potentially extract the Zero-point energy of the electromagnetic field and nuclear forces in the form of gravitational waves.[269] In the spheron model of the nucleus,[270] proposed by the two times Nobel laureate Linus Pauling, dineutrons are among the components of this structure. Similarly to a dumbbell put in a suitable rotational state, but with nuclear mass density, dineutrons are nearly ideal sources of gravitational waves at X-ray and gamma-ray frequencies. The dynamical interplay, mediated by nuclear forces, between the electrically neutral dineutrons and the electrically charged core nucleus is the fundamental mechanism by which nuclear vibrations can be converted to a rotational state of dineutrons with emission of gravitational waves. Gravity and gravitational waves are well described by General Relativity, that is not a quantum theory, this implies that there is no Zero-point energy for gravity in this theory, therefore dineutrons will emit gravitational waves like any other known source of gravitational waves. In Fontana and Binder paper, nuclear species with dynamical instabilites, related to the Zero-point energy of the electromagnetic field and nuclear forces, and possessing dineutrons, will emit gravitational waves. In experimental physics this approach is still unexplored.
In 2014 NASA's Eagleworks Laboratories announced that they had successfully validated the use of a Quantum Vacuum Plasma Thruster which makes use of the Casimir effect for propulsion.[271][272][273] In 2016 a scientific paper by the team of NASA scientists passed peer review for the first time.[274] The paper suggests that the zero-point field acts as pilot-wave and that the thrust may be due to particles pushing off the quantum vacuum. While peer review doesn't guarantee that a finding or observation is valid, it does indicate that independent scientists looked over the experimental setup, results, and interpretation and that they could not find any obvious errors in the methodology and that they found the results reasonable. In the paper, the authors identify and discuss nine potential sources of experimental errors, including rogue air currents, leaky electromagnetic radiation, and magnetic interactions. Not all of them could be completely ruled out, and further peer-reviewed experimentation is needed in order to rule these potential errors out.[275]
See also
- Casimir effect
- Ground state
- Lamb shift
- QED vacuum
- QCD vacuum
- Quantum fluctuation
- Quantum foam
- Scalar field
- Time crystal
- Topological order
- Unruh effect
- Vacuum energy
- Vacuum expectation value
- Vacuum state
- Virtual particle
References
Notes
- ↑ 1.0 1.1 1.2 Sciama (1991), p. 137.
- ↑ 2.0 2.1 2.2 Milonni (1994), p. 35.
- ↑ Davies (2011).
- ↑ See Weinberg (1989) and Peebles & Ratra (2003) for review articles and Shiga (2005), Siegel (2016) for press comment
- ↑ 5.0 5.1 Weinberg (2015), p. 376.
- ↑ 6.0 6.1 Sciama (1991), p. 138.
- ↑ 7.0 7.1 Davies (1985), p. 104.
- ↑ Einstein (1995), pp. 270–285.
- ↑ 9.0 9.1 Battersby (2008).
- ↑ 10.0 10.1 Itzykson & Zuber (1980), p. 111.
- ↑ 11.0 11.1 11.2 Milonni (1994), p. 111.
- ↑ Greiner, Müller & Rafelski (2012), p. 12.
- ↑ Bordag et al. (2009), p. 4.
- ↑ Cho (2015).
- ↑ Choi (2013).
- ↑ 16.0 16.1 See Haisch, Rueda & Puthoff (1994) for proposal and Matthews (1994, 1995), Powell (1994) and Davies (1994) for comment.
- ↑ See Urban et al. (2013), Leuchs & Sánchez-Soto (2013) and O'Carroll (2013) for comment.
- ↑ 18.0 18.1 18.2 Rugh & Zinkernagel (2002).
- ↑ 19.0 19.1 "Dark Energy May Be Vacuum" (Press release). Niels Bohr Institute. 19 January 2007. Archived from the original on 31 May 2017.
- ↑ 20.0 20.1 Wall (2014).
- ↑ Saunders & Brown (1991), p. 1.
- ↑ Conlon (2011), p. 225.
- ↑ Kragh & Overduin (2014), p. 7.
- ↑ Planck (1900).
- ↑ Loudon (2000), p. 9.
- ↑ 26.0 26.1 Kragh (2012), p. 7.
- ↑ Planck (1912a).
- ↑ Milonni (1994), p. 10.
- ↑ See (Planck 1911, 1912a, 1912b, 1913) and Planck (1958) for reprints
- ↑ Kuhn (1978), p. 235.
- ↑ Einstein, Albert; Stern, Otto (1913). "Einige Argumente für die Annahme einer molekularen Agitation beim absoluten Nullpunkt" (in de). Annalen der Physik 345 (3): 551–560. doi:10.1002/andp.19133450309. Bibcode: 1913AnP...345..551E. https://zenodo.org/record/1424262.
- ↑ Einstein (1993), pp. 563–565.
- ↑ Debye, Peter (1913). "Interferenz von Röntgenstrahlen und Wärmebewegung" (in de). Annalen der Physik 348 (1): 49–92. doi:10.1002/andp.19133480105. Bibcode: 1913AnP...348...49D. https://zenodo.org/record/1424272.
- ↑ Nernst, Walther (1916). "Über einen Versuch, von quantentheoretischen Betrachtungen zur Annahme stetiger Energieänderungen zurückzukehren" (in de). Verhandlungen der Deutschen Physikalischen 18: 83–116.
- ↑ Einstein, Albert (1920) (in de). Äther und Relativitäts-Theorie. Berlin: Springer.
- ↑ Einstein, Albert (1922). Jeffery, G. B.; Perrett, W.. eds. Sidelights on Relativity: Ether and the Theory of Relativity. New York: Methuen & Co. pp. 1–24. https://archive.org/details/sidelightsonrela00einsuoft.
- ↑ Bennewitz, Kurt; Simon, Franz (1923). "Zur Frage der Nullpunktsenergie" (in de). Zeitschrift für Physik 16 (1): 183–199. doi:10.1007/BF01327389. Bibcode: 1923ZPhy...16..183B.
- ↑ Simon, F. (1934). "Behaviour of Condensed Helium near Absolute Zero". Nature 133 (3362): 529. doi:10.1038/133529a0. Bibcode: 1934Natur.133Q.529S.
- ↑ Dugdale, J. S.; Simon, F. E. (1953). "Thermodynamic Properties and Melting of Solid Helium". Proceedings of the Royal Society 218 (1134): 291. doi:10.1098/rspa.1953.0105. Bibcode: 1953RSPSA.218..291D.
- ↑ Mulliken, Robert S. (1924). "The band spectrum of boron monoxide". Nature 114 (2862): 349–350. doi:10.1038/114349a0. Bibcode: 1924Natur.114..349M.
- ↑ Heisenberg, W. (1925). "Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen". in Blum, Walter (in de). Wissenschaftliche Originalarbeiten. Berlin, Heidelberg: Springer. 1985. pp. 382–396. doi:10.1007/978-3-642-61659-4_26. ISBN 978-3-642-64900-4. OCLC 7331244990.
- ↑ Kragh (2002), p. 162.
- ↑ Bohr, Niels (1913). "On the Constitution of Atoms and Molecules, Part I". Philosophical Magazine 26 (151): 1–24. doi:10.1080/14786441308634955. Bibcode: 1913PMag...26....1B. http://web.ihep.su/dbserv/compas/src/bohr13/eng.pdf.
- ↑ Bohr, Niels (1913). "On the Constitution of Atoms and Molecules, Part II Systems Containing Only a Single Nucleus". Philosophical Magazine 26 (153): 476–502. doi:10.1080/14786441308634993. Bibcode: 1913PMag...26..476B. http://web.ihep.su/dbserv/compas/src/bohr13b/eng.pdf.
- ↑ Bohr, Niels (1913). "On the Constitution of Atoms and Molecules, Part III Systems containing several nuclei". Philosophical Magazine 26 (155): 857–875. doi:10.1080/14786441308635031. Bibcode: 1913PMag...26..857B. https://zenodo.org/record/1430922.
- ↑ Jeans, James Hopwood (1915). The mathematical theory of electricity and magnetism (3rd ed.). Cambridge: Cambridge University Press. p. 168. https://archive.org/details/cu31924012330589.
- ↑ Schrödinger, Erwin (1926). "Quantisierung als Eigenwertproblem" (in de). Annalen der Physik 79 (13): 361–376. doi:10.1002/andp.19263851302. Bibcode: 1926AnP...385..437S.
- ↑ Lieb, E. H.; Seiringer, R. (2009). The Stability of Matter in Quantum Mechanics. Cambridge: Cambridge University Press. pp. 2–3. ISBN 978-0-521-19118-0. OCLC 638472161. https://archive.org/details/stabilitymatterq00hlie.
- ↑ Born, M.; Heisenberg, W.; Jordan, P. (1926). "Zur Quantenmechanik. II" (in de). Zeitschrift für Physik 35 (8): 557–615. doi:10.1007/BF01379806. Bibcode: 1926ZPhy...35..557B.
- ↑ Einstein, Albert (1909). "Zum gegenwärtigen Stand des Strahlungsproblems". Physikalische Zeitschrift 10: 185–193. Bibcode: 1909PhyZ...10..185E.
- ↑ Mehra, J.; Rechenberg, H. (2002). The Historical Development of Quantum Theory. 6. Springer. p. 57. ISBN 978-0-387-95262-8. OCLC 722601833.
- ↑ Jordan, P.; Pauli, W. (1928). "Zur Quantenelektrodynamik ladungsfreier Felder" (in de). Zeitschrift für Physik 47 (3): 151–173. doi:10.1007/BF02055793. Bibcode: 1928ZPhy...47..151J.
- ↑ Schweber, Silvan S. (1994). QED and the Men Who Made It: Dyson, Feynman, Schwinger and Tomonaga. Princeton University Press. pp. 108–112. ISBN 978-0-691-03327-3. OCLC 439849774. https://archive.org/details/qedmenwhomadeitd0000schw.
- ↑ 54.0 54.1 54.2 Dirac (1927).
- ↑ Weinberg, Steven (1977). "The Search for Unity: Notes for a History of Quantum Field Theory". Daedalus 106 (4): 17–35.
- ↑ Yokoyama, H.; Ujihara, K. (1995). Spontaneous emission and laser oscillation in microcavities. Boca Raton: CRC Press. p. 6. ISBN 978-0-8493-3786-4. OCLC 832589969.
- ↑ Scully & Zubairy (1997), §1.5.2 pp. 22–23.
- ↑ Weisskopf, Viktor (1935). "Probleme der neueren Quantentheorie des Elektrons" (in de). Naturwissenschaften 23 (37): 631–637. doi:10.1007/BF01492012. Bibcode: 1935NW.....23..631W.
- ↑ Welton, Theodore Allen (1948). "Some observable effects of the quantum-mechanical fluctuations of the electromagnetic field". Physical Review 74 (9): 1157. doi:10.1103/PhysRev.74.1157. Bibcode: 1948PhRv...74.1157W.
- ↑ Lamb, Willis; Retherford, Robert (1947). "Fine Structure of the Hydrogen Atom by a Microwave Method". Physical Review 72 (3): 241–243. doi:10.1103/PhysRev.72.241. Bibcode: 1947PhRv...72..241L.
- ↑ Foley, H.; Kusch, P. (1948). "On the Intrinsic Moment of the Electron". Physical Review 73 (3): 412. doi:10.1103/PhysRev.73.412. Bibcode: 1948PhRv...73..412F.
- ↑ Dresden, M. (1987). H. A. Kramers: Between Tradition and Revolution. New York: Springer. ISBN 978-1-461-29087-2. OCLC 1015092892.
- ↑ Weisskopf (1936), p. 6.
- ↑ Bethe, Hans Albrecht (1947). "The Electromagnetic Shift of Energy Levels". Physical Review 72 (4): 339. doi:10.1103/PhysRev.72.339. Bibcode: 1947PhRv...72..339B.
- ↑ Power (1964), p. 35.
- ↑ Pauli, Wolfgang (1946). "Exclusion principle and quantum mechanics". Royal Swedish Academy of Sciences. https://www.nobelprize.org/nobel_prizes/physics/laureates/1945/pauli-lecture.pdf.
- ↑ Casimir, Hendrik Brugt Gerhard; Polder, Dirk (1948). "The Influence of Retardation on the London–Van der Waals Forces". Physical Review 73 (4): 360. doi:10.1103/PhysRev.73.360. Bibcode: 1948PhRv...73..360C.
- ↑ Casimir, Hendrik Brugt Gerhard (1948). "On the attraction between two perfectly conducting plates". Proceedings of the Royal Netherlands Academy of Arts and Sciences 51: 793–795. http://www.dwc.knaw.nl/DL/publications/PU00018547.pdf. Retrieved 19 October 2016.
- ↑ Eisenschitz, R.; London, F. (1930). "Über das Verhältnis der Van der Waalsschen Kräfte zu den homöopolaren Bindungskräften" (in de). Zeitschrift für Physik 60 (7–8): 491–527. doi:10.1007/BF01341258. Bibcode: 1930ZPhy...60..491E.
- ↑ London, F. (1930). "Zur Theorie und Systematik der Molekularkräfte" (in de). Zeitschrift für Physik 63 (3–4): 245. doi:10.1007/BF01421741. Bibcode: 1930ZPhy...63..245L.
- ↑ Lambrecht, Astrid (2002). "The Casimir effect: a force from nothing". Physics World (Institute of Physics Publishing) 15 (9): 29–32. doi:10.1088/2058-7058/15/9/29. ISSN 0953-8585. https://indico.cern.ch/event/247728/contributions/1569920/attachments/426300/591724/Casimir_Force_PhysWorld_2002.pdf. Retrieved 24 October 2016.
- ↑ Lifshitz, E. M. (1954). "The Theory of Molecular Attractive Forces between Solids". Journal of Experimental Theoretical Physics USSR 29: 94–110.
- ↑ Lifshitz, E. M. (1956). "The theory of molecular Attractive Forces between Solids". Soviet Physics 2 (1): 73–83.
- ↑ Derjaguin, B. V.; Abrikosova, I. I.; Lifshitz, E. M. (1956). "Direct measurement of molecular attraction between solids separated by a narrow gap". Quarterly Reviews, Chemical Society 10 (3): 295–329. doi:10.1039/qr9561000295.
- ↑ Mahanty, J.; Ninham, B. W. (1976). Dispersion Forces. Academic Press. ISBN 978-0-124-65050-3. OCLC 925046024.
- ↑ 76.0 76.1 76.2 Callen, Herbert; Welton, Theodore A. (1951). "Irreversibility and Generalized Noise". Physical Review 83 (1): 34–40. doi:10.1103/PhysRev.83.34. Bibcode: 1951PhRv...83...34C.
- ↑ 77.0 77.1 Nyquist, Harry (1928). "Thermal Agitation of Electric Charge in Conductors". Physical Review 32 (1): 110–113. doi:10.1103/PhysRev.32.110. Bibcode: 1928PhRv...32..110N.
- ↑ 78.0 78.1 Johnson, John Bertrand (1928). "Thermal Agitation of Electricity in Conductors". Physical Review 32 (1): 97–109. doi:10.1103/PhysRev.32.97. Bibcode: 1928PhRv...32...97J.
- ↑ 79.0 79.1 Milonni (1994), p. 54.
- ↑ 80.0 80.1 Koch, Roger H.; Van Harlingen, D. J.; Clarke, John (1981). "Observation of Zero-Point Fluctuations in a Resistively Shunted Josephson Tunnel Junction". Physical Review Letters 47 (17): 1216–1219. doi:10.1103/PhysRevLett.47.1216. Bibcode: 1981PhRvL..47.1216K. https://cloudfront.escholarship.org/dist/prd/content/qt7cb912p9/qt7cb912p9.pdf?t=maz7le.
- ↑ 81.0 81.1 Allahverdyan, A. E.; Nieuwenhuizen, Th. M. (2000). "Extraction of Work from a Single Thermal Bath in the Quantum Regime". Physical Review Letters 85 (9): 1799–1802. doi:10.1103/PhysRevLett.85.1799. PMID 10970617. Bibcode: 2000PhRvL..85.1799A. https://pure.uva.nl/ws/files/3031844/12613_88222y.pdf.
- ↑ 82.0 82.1 Scully et al. (2003).
- ↑ Jaynes, E. T.; Cummings, F. W. (1963). "Comparison of quantum and semiclassical radiation theories with application to the beam maser". Proceedings of the IEEE 51 (1): 89–109. doi:10.1109/PROC.1963.1664.
- ↑ Drexhage (1970).
- ↑ Drexhage (1974), p. [page needed].
- ↑ Hulet, Randall G.; Hilfer, Eric S.; Kleppner, Daniel (1985). "Inhibited Spontaneous Emission by a Rydberg Atom". Physical Review Letters 55 (20): 2137–2140. doi:10.1103/PhysRevLett.55.2137. PMID 10032058. Bibcode: 1985PhRvL..55.2137H. https://scholarship.rice.edu/bitstream/1911/79433/1/PhysRevLett.55.2137.pdf.
- ↑ Yablonovitch, Eli (1987). "Inhibited Spontaneous Emission in Solid-State Physics and Electronics". Physical Review Letters 58 (20): 2059–2062. doi:10.1103/PhysRevLett.58.2059. PMID 10034639. Bibcode: 1987PhRvL..58.2059Y.
- ↑ Purcell, E. M. (1946). "Proceedings of the American Physical Society". Physical Review 69 (11–12): 674. doi:10.1103/PhysRev.69.674. Bibcode: 1946PhRv...69Q.674..
- ↑ Goy et al. (1983).
- ↑ Milonni (1983).
- ↑ Heisenberg, W. (1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik" (in de). Zeitschrift für Physik 43 (3): 172–198. doi:10.1007/BF01397280. Bibcode: 1927ZPhy...43..172H. http://scarc.library.oregonstate.edu/coll/pauling/bond/papers/corr155.1.html.
- ↑ Gribbin, J. R. (1998). Gribbin, M.. ed. Q is for Quantum: An Encyclopedia of Particle Physics. Touchstone Books. ISBN 978-0-684-86315-3. OCLC 869069919. Bibcode: 1999qqep.book.....G.
- ↑ Peskin & Schroeder (1995), pp. 786–791.
- ↑ Milonni (1994), pp. 73–74.
- ↑ Wheeler, John Archibald (1955). "Geons". Physical Review 97 (2): 511. doi:10.1103/PhysRev.97.511. Bibcode: 1955PhRv...97..511W.
- ↑ Power (1964), pp. 31–33.
- ↑ 97.0 97.1 Milonni (1981).
- ↑ 98.0 98.1 Senitzky, I. R. (1960). "Dissipation in Quantum Mechanics. The Harmonic Oscillator". Physical Review 119 (2): 670. doi:10.1103/PhysRev.119.670. Bibcode: 1960PhRv..119..670S.
- ↑ "Higgs bosons: theory and searches". Particle Data Group. 12 July 2012. http://pdg.lbl.gov/2012/reviews/rpp2012-rev-higgs-boson.pdf.
- ↑ Milonni (1994), pp. 42–43.
- ↑ Peskin & Schroeder (1995), p. 22.
- ↑ Milonni (2009), p. 865.
- ↑ 103.0 103.1 Abbott, Larry (1988). "The Mystery of the Cosmological Constant". Scientific American 258 (5): 106–113. doi:10.1038/scientificamerican0588-106. Bibcode: 1988SciAm.258e.106A. http://pages.erau.edu/~reynodb2/blog/Abbott_CosmologicalConstant_SciAm.pdf.
- ↑ Derjaguin, B. V.; Abrikosova, I. I.; Lifshitz, E. M. (1956). "Direct measurement of molecular attraction between solids separated by a narrow gap". Quarterly Reviews, Chemical Society 10 (3): 295–329. doi:10.1039/QR9561000295.
- ↑ Sparnaay, M. J. (1958). "Measurements of attractive forces between flat plates". Physica 24 (6–10): 751–764. doi:10.1016/S0031-8914(58)80090-7. Bibcode: 1958Phy....24..751S.
- ↑ Tabor, D.; Winterton, R. H. S. (1968). "Surface Forces: Direct Measurement of Normal and Retarded Van der Waals Forces". Nature 219 (5159): 1120–1121. doi:10.1038/2191120a0. PMID 5675624. Bibcode: 1968Natur.219.1120T.
- ↑ Hunklinger, S.; Geisselmann, H.; Arnold, W. (1972). "A Dynamic Method for Measuring the Van der Waals Forces between Macroscopic Bodies". Rev. Sci. Instrum. 43 (4): 584–587. doi:10.1063/1.1685696. Bibcode: 1972RScI...43..584H.
- ↑ Van Blokland, Peter H. G. M.; Overbeek, J. Theodoor G. (1978). "Van der Waals forces between objects covered with a chromium layer". J. Chem. Soc., Faraday Trans. 1 74: 2637–2651. doi:10.1039/F19787402637.
- ↑ Lamoreaux, S. K. (1997). "Demonstration of the Casimir Force in the 0.6 to 6 μm Range". Physical Review Letters 78 (1): 5–8. doi:10.1103/PhysRevLett.78.5. Bibcode: 1997PhRvL..78....5L. http://web.mit.edu/~kardar/www/research/seminars/Casimir/PRL-Lamoreaux.pdf.
- ↑ Mohideen, Umar; Roy, Anushree (1998). "Precision Measurement of the Casimir Force from 0.1 to 0.9 μm". Physical Review Letters 81 (21): 4549–4552. doi:10.1103/PhysRevLett.81.4549. Bibcode: 1998PhRvL..81.4549M.
- ↑ 111.0 111.1 Chan et al. (2001).
- ↑ Bressi et al. (2002).
- ↑ Decca et al. (2003).
- ↑ Munday, J. N.; Capasso, Federico; Parsegian, V. Adrian (2009). "Measured long-range repulsive Casimir–Lifshitz forces". Nature 457 (7226): 170–173. doi:10.1038/nature07610. PMID 19129843. PMC 4169270. Bibcode: 2009Natur.457..170M. http://nanoqed.synthasite.com/resources/nature07610.pdf.
- ↑ Dzyaloshinskii, I. E.; Lifshitz, E. M.; Pitaevskii, Lev P. (1961). "General Theory of Van der Waals' Forces". Soviet Physics Uspekhi 4 (2): 154. doi:10.1070/PU1961v004n02ABEH003330. Bibcode: 1961SvPhU...4..153D.
- ↑ Capasso et al. (2007).
- ↑ 117.0 117.1 See Barton & Scharnhorst (1993) and Chown (1990)
- ↑ Itzykson & Zuber (1980), p. 80.
- ↑ Hawton, M. (1993). "Self-consistent frequencies of the electron–photon system". Physical Review A 48 (3): 1824–1831. doi:10.1103/PhysRevA.48.1824. PMID 9909797. Bibcode: 1993PhRvA..48.1824H.
- ↑ Le Bellac (2006), p. 381.
- ↑ Le Bellac (2006), p. 33.
- ↑ Aitchison, Ian; Hey, Anthony (2012). Gauge Theories in Particle Physics: A Practical Introduction: Volume 1: From Relativistic Quantum Mechanics to QED (4th ed.). CRC Press. p. 343. ISBN 9781466512993.
- ↑ Quigg, C (1998). Espriu, D; Pich, A. eds. Advanced School on Electroweak Theory: Hadron Colliders, the Top Quark, and the Higgs Sector. World Scientific. p. 143. ISBN 9789814545143.
- ↑ Heisenberg & Euler (1936).
- ↑ Weisskopf (1936), p. 3.
- ↑ Greiner, Müller & Rafelski (2012), p. 278.
- ↑ Greiner, Müller & Rafelski (2012), p. 291.
- ↑ See Dunne (2012) for a historical review of the subject.
- ↑ Heyl & Shaviv (2000), p. 1.
- ↑ See Carroll & Field (1997) and Kostelecký and Mewes (2009, 2013) for an overview of this area.
- ↑ See Mignani et al. (2017) for experiment and Cho (2016), Crane (2016) and Bennett (2016) for comment.
- ↑ Rees (2012), p. 528.
- ↑ Crane (2016).
- ↑ Cho (2016).
- ↑ Battersby (2016).
- ↑ Riess et al. (1998).
- ↑ Perlmutter et al. (1998).
- ↑ Clark, Stuart (2016). "The Universe is Flat as a Pancake". New Scientist 232 (3097): 35. https://archive.org/details/NewScientistOctober29/page/n35/mode/2up.
- ↑ Miller, Katrina (2023-07-01). "The Dark Universe Is Waiting. What Will the Euclid Telescope Reveal?" (in en). The New York Times. https://www.nytimes.com/2023/07/01/science/spacex-euclid-launch.html.
- ↑ Carroll, Sean M. (1998). "Quintessence and the Rest of the World: Suppressing Long-Range Interactions". Physical Review Letters 81 (15): 3067–3070. doi:10.1103/PhysRevLett.81.3067. ISSN 0031-9007. Bibcode: 1998PhRvL..81.3067C. https://cds.cern.ch/record/356711/files/9806099.pdf.
- ↑ Tyson, Neil deGrasse and Donald Goldsmith (2004), Origins: Fourteen Billion Years of Cosmic Evolution, W. W. Norton & Co., pp. 84–85.
- ↑ Enz, Charles P. (1974). Enz, C. P.; Mehra, J.. eds. Physical Reality and Mathematical Description Is the Zero-Point Energy Real?. Dordrecht: D. Reidel Publishing Company. pp. 124–132. doi:10.1007/978-94-010-2274-3. ISBN 978-94-010-2274-3.
- ↑ See Schwinger (1998a, 1998b, 1998c)
- ↑ Schwinger, Julian (1975). "Casimir effect in source theory". Letters in Mathematical Physics 1 (1): 43–47. doi:10.1007/BF00405585. Bibcode: 1975LMaPh...1...43S.
- ↑ Schwinger, Julian; DeRaad, Lester L.; Milton, Kimball A. (1978). "Casimir effect in dielectrics". Annals of Physics 115 (1): 1–23. doi:10.1016/0003-4916(78)90172-0. Bibcode: 1978AnPhy.115....1S.
- ↑ Jaffe, R. L. (2005). "Casimir effect and the quantum vacuum". Physical Review D 72 (2): 021301. doi:10.1103/PhysRevD.72.021301. Bibcode: 2005PhRvD..72b1301J.
- ↑ Milonni (1994), p. 48.
- ↑ Greiner, Müller & Rafelski (2012), p. 20.
- ↑ Barrett, Terence W. (2008). Topological Foundations of Electromagnetism. Singapore: World Scientific. p. 2. ISBN 9789812779977. https://books.google.com/books?id=e0-QdLqT-pIC.
- ↑ Greiner, Müller & Rafelski (2012), p. 23.
- ↑ Ehrenberg, W; Siday, RE (1949). "The Refractive Index in Electron Optics and the Principles of Dynamics". Proceedings of the Physical Society. Series B 62 (1): 8–21. doi:10.1088/0370-1301/62/1/303. Bibcode: 1949PPSB...62....8E.
- ↑ Aharonov, Y; Bohm, D (1959). "Significance of electromagnetic potentials in quantum theory". Physical Review 115 (3): 485–491. doi:10.1103/PhysRev.115.485. Bibcode: 1959PhRv..115..485A.
- ↑ Altshuler, B. L.; Aronov, A. G.; Spivak, B. Z. (1981). "The Aaronov-Bohm effect in disordered conductors". Pisma Zh. Eksp. Teor. Fiz. 33: 101. Bibcode: 1981JETPL..33...94A. http://www.jetpletters.ac.ru/ps/1501/article_22943.pdf. Retrieved 3 November 2016.
- ↑ Berry, M. V. (1984). "Quantal Phase Factors Accompanying Adiabatic Changes". Proc. R. Soc. A392 (1802): 45–57. doi:10.1098/rspa.1984.0023. Bibcode: 1984RSPSA.392...45B.
- ↑ Aharonov, Y.; Anandan, J. (1987). "Phase change during a cyclic quantum evolution". Physical Review Letters 58 (16): 1593–1596. doi:10.1103/PhysRevLett.58.1593. PMID 10034484. Bibcode: 1987PhRvL..58.1593A.
- ↑ Pancharatnam, S. (1956). "Generalized theory of interference, and its applications". Proceedings of the Indian Academy of Sciences 44 (5): 247–262. doi:10.1007/BF03046050.
- ↑ Chiao, Raymond Y.; Wu, Yong-Shi (1986). "Manifestations of Berry's Topological Phase for the Photon". Physical Review Letters 57 (8): 933–936. doi:10.1103/PhysRevLett.57.933. PMID 10034203. Bibcode: 1986PhRvL..57..933C.
- ↑ B. D. Josephson (1962). "Possible new effects in superconductive tunnelling". Phys. Lett. 1 (7): 251–253. doi:10.1016/0031-9163(62)91369-0. Bibcode: 1962PhL.....1..251J.
- ↑ B. D. Josephson (1974). "The discovery of tunnelling supercurrents". Rev. Mod. Phys. 46 (2): 251–254. doi:10.1103/RevModPhys.46.251. Bibcode: 1974RvMP...46..251J. https://www.europhysicsnews.org/10.1051/epn/19740503001/pdf.
- ↑ K. v. Klitzing; G. Dorda; M. Pepper (1980). "New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance". Physical Review Letters 45 (6): 494–497. doi:10.1103/PhysRevLett.45.494. Bibcode: 1980PhRvL..45..494K.
- ↑ De Haas, W. J.; Van Alphen, P. M. (1930). "The dependance of the susceptibility of diamagnetic metals upon the field". Proc. Netherlands R. Acad. Sci. 33: 1106.
- ↑ Penrose (2004), pp. 453–454.
- ↑ Feng, J. H.; Kneubühl, F. K. (1995). Barrett, Terence William; Grimes, Dale M.. eds. Solitons and Chaos in Periodic Nonlinear Optical Media and Lasers: Advanced Electromagnetism: Foundations, Theory and Applications. Singapore: World Scientific. p. 438. ISBN 978-981-02-2095-2. https://books.google.com/books?id=OdnsCgAAQBAJ.
- ↑ Hunt, Bruce J. (2005). The Maxwellians. Cornell: Cornell University Press. p. 17. ISBN 9780801482342. https://books.google.com/books?id=23rBH11Q9w8C.
- ↑ Josephs, H.J. (1959). "The Heaviside papers found at Paignton in 1957". Proceedings of the IEE - Part C: Monographs 106 (9): 70. doi:10.1049/pi-c.1959.0012.
- ↑ Hunt, Bruce J. (2005). The Maxwellians. Cornell: Cornell University Press. pp. 165–166. ISBN 9780801482342. https://books.google.com/books?id=23rBH11Q9w8C.
- ↑ Barrett, T. W. (1991). "Tesla's Nonlinear Oscillator-Shuttle-Circuit (OSC) Theory". Annales de la Fondation Louis de Broglie 16 (1): 23–41. ISSN 0182-4295. http://www.cheniere.org/references/TeslaOSC.pdf. Retrieved 3 November 2016.
- ↑ Penrose (2004), p. 201.
- ↑ Rocher, E. Y. (1972). "Noumenon: Elementary entity of a new mechanics". J. Math. Phys. 13 (12): 1919. doi:10.1063/1.1665933. Bibcode: 1972JMP....13.1919R.
- ↑ Imaeda, K. (1976). "A new formulation of classical electrodynamics". Il Nuovo Cimento B 32 (1): 138–162. doi:10.1007/BF02726749. Bibcode: 1976NCimB..32..138I.
- ↑ Kauffmann, T.; Sun, Wen IyJ (1993). "Quaternion mechanics and electromagnetism". Annales de la Fondation Louis de Broglie 18 (2): 213–219.
- ↑ Lambek, Joachim. "QUATERNIONS AND THREE TEMPORAL DIMENSIONS". https://www.math.mcgill.ca/barr/lambek/pdffiles/Quater2014.pdf.
- ↑ Bostick et al. (1966).
- ↑ Ferraro, V .; Plumpton, C. (1961). An Introduction to Magneto-Fluid Mechanics. Oxford: Oxford University Press. https://archive.org/details/introductiontoma00ferr.
- ↑ White, Carol (1977). Energy potential: Toward a new electro-magnetic field theory. New York: Campaigner Pub.. ISBN 978-0918388049.
- ↑ Noether, E. (1918). "Invariante Variationsprobleme". Nachr. D. König. Gesellsch. D. Wiss. Zu Göttingen, Math-phys. Klasse 1918: 235–257.
- ↑ Scott (2006), p. 163.
- ↑ Pismen, L. M. (2006). Patterns and Interfaces in Dissipative Dynamics. Springer. p. 3. ISBN 9783540304319. https://books.google.com/books?id=Wje3RXlQdaMC.
- ↑ "The Nobel Prize in Chemistry 1977". Royal Swedish Academy of Sciences. 1977. https://www.nobelprize.org/nobel_prizes/chemistry/laureates/1977/.
- ↑ Nicolis, G.; Prigogine, I. (1977). Self-organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations. Wiley-Blackwell. ISBN 978-0471024019.
- ↑ Prigogine, Ilya; Stengers, Isabelle (1984). Order out of Chaos. Flamingo. ISBN 978-0-00-654115-8.
- ↑ Gleick, James (1987). Chaos: Making a New Science (1998 ed.). Vintage. p. 308. ISBN 9780749386061.
- ↑ Chaisson, Eric J. (2002). Cosmic Evolution: The Rise of Complexity in Nature. Harvard University Press. p. 139. ISBN 978-0674009875. https://books.google.com/books?id=KG2SZouhFuIC.
- ↑ Kais, Sabre (2011). Popelier, Paul. ed. Finite Size Scaling for Criticality of the Schrödinger Equation: Solving the Schrödinger Equation: Has Everything Been Tried?. Singapore: Imperial College Press. pp. 91–92. ISBN 978-1-84816-724-7. https://books.google.com/books?id=zFK7CgAAQBAJ.
- ↑ "Classical Physics Makes a Comeback". The Times (London). 14 January 1982.
- ↑ Bostick, W. (1985). "On the Controversy over Whether Classical Systems Like Plasmas Can Behave Like Superconductors (Which Have Heretofore Been Supposed to Be Strictly Quantum Mechanically Dominated)". International Journal of Fusion Energy 3 (2): 47–51. https://wlym.com/archive/fusion/ijfe/19850404-IJFE.pdf. Retrieved 2020-05-22.
- ↑ Bostick, W. (1985). "The Morphology of the Electron". International Journal of Fusion Energy 3 (1): 9–52. http://wlym.com/archive/fusion/ijfe/19850101-IJFE.pdf. Retrieved 2020-05-22.
- ↑ Bostick, W. (1985). "Recent Experimental Results of The Plasma-Focus Group at Darmstadt, West Germany: A Review and Critique". International Journal of Fusion Energy 3 (1): 68. http://wlym.com/archive/fusion/ijfe/19850101-IJFE.pdf. Retrieved 2020-05-22.
- ↑ Edwards, W. Farrell (1981). "Classical Derivation of the London Equations". Physical Review Letters 47 (26): 1863–1866. doi:10.1103/PhysRevLett.47.1863. Bibcode: 1981PhRvL..47.1863E.
- ↑ Fröhlich, H (1966). "Macroscopic wave functions in superconductors". Proceedings of the Physical Society 87 (1): 330–332. doi:10.1088/0370-1328/87/1/137. Bibcode: 1966PPS....87..330F.
- ↑ Reed (1995), p. 226.
- ↑ Chen, Xie; Gu, Zheng-Cheng; Wen, Xiao-Gang (2010). "Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order". Physical Review B 82 (15): 155138. doi:10.1103/PhysRevB.82.155138. Bibcode: 2010PhRvB..82o5138C.
- ↑ Chaisson, Eric J. (2005). "2 Non-equilibrium Thermodynamics in an Energy-Rich Universe". Non-equilibrium Thermodynamics in an Energy-Rich Universe. Understanding Complex Systems. pp. 21–31. doi:10.1007/11672906_2. ISBN 978-3-540-22495-2.
- ↑ Chaisson, Eric J. (2002). Cosmic Evolution: The Rise of Complexity in Nature. Harvard University Press. p. 216. ISBN 978-0674009875. https://books.google.com/books?id=KG2SZouhFuIC.
- ↑ Peterson, I (1997). "Peeking inside an electron's screen". Science News 151: 89. https://www.sciencenews.org/archive/physics-5. Retrieved 24 October 2016.
- ↑ 196.0 196.1 196.2 Amber M. Aiken. "Zero-Point Energy: Can We Get Something From Nothing?". U.S. Army National Ground Intelligence Center. http://info.publicintelligence.net/USArmy-ZeroPointEnergy.pdf. "Forays into "free energy" inventions and perpetual-motion machines using ZPE are considered by the broader scientific community to be pseudoscience."
- ↑ "Zero-point energy, on season 8 , episode 2". Scientific American Frontiers. Chedd-Angier Production Company. 1997–1998. PBS. Archived from the original on 2006.
- ↑ 198.0 198.1 Scott (2004).
- ↑ Forward, Robert L. (1985). "Extracting electrical energy from the vacuum by cohesion of charged foliated conductors". Physical Review B 30 (4): 1700. doi:10.1103/PhysRevB.30.1700. Bibcode: 1984PhRvB..30.1700F.
- ↑ Serry, F. M.; Walliser, D.; Maclay, G. J. (1995). "The anharmonic Casimir oscillator (ACO)-the Casimir effect in a model microelectromechanical system". Journal of Microelectromechanical Systems 4 (4): 193–205. doi:10.1109/84.475546. http://www.quantumfields.com/IEEEJMEMSACO.pdf. Retrieved 24 October 2016.
- ↑ Serry, F. Michael; Walliser, Dirk; Maclay, G. Jordan (1998). "The role of the casimir effect in the static deflection and stiction of membrane strips in microelectromechanical systems (MEMS)". Journal of Applied Physics 84 (5): 2501–2506. doi:10.1063/1.368410. Bibcode: 1998JAP....84.2501S. https://www.mit.edu/~kardar/research/seminars/Casimir/SerryMEMS.pdf. Retrieved 24 October 2016.
- ↑ Bordag et al. (2009), p. [page needed].
- ↑ Pinto (1999).
- ↑ Scandurra, M. (2001). "Thermodynamic properties of the quantum vacuum". arXiv:hep-th/0104127.
- ↑ Moddel, Garret; Dmitriyevaa, Olga (2009). "Extraction of Zero-Point Energy from the Vacuum: Assessment of Stochastic Electrodynamics-Based Approach as Compared to Other Methods". Atoms 7 (2): 51. doi:10.3390/atoms7020051.
- ↑ "DARPA-BAA-08-59". DARPA. 2008. https://www.fbo.gov/index?id=0bb7cc8cf76384af4cc4732914ac55ce.
- ↑ U.S. Patent 7,379,286
- ↑ Dmitriyevaa, Olga; Moddel, Garret (2012). "Test of zero-point energy emission from gases flowing through Casimir cavities". Physics Procedia 38: 8–17. doi:10.1016/j.phpro.2012.08.007. Bibcode: 2012PhPro..38....8D. http://ecee.colorado.edu/~moddel/QEL/Papers/DmitriyevaModdel12.pdf. Retrieved 1 November 2016.
- ↑ Henriques, Carlos (2014). Study of atomic energy shifts induced by Casimir cavities (Thesis for: MS). Advisors: Fernandes, Luis & Amaro, F. doi:10.13140/RG.2.1.4297.1608.
- ↑ MacDonald, D.K.C. (1962). "On Brownian Movement and irreversibility". Physica 28 (4): 409–416. doi:10.1016/0031-8914(62)90019-8. Bibcode: 1962Phy....28..409M.
- ↑ Harris, I. A. (1971). "Zero-point fluctuations and thermal-noise standards". Electron. Lett. 7 (7): 148–149. doi:10.1049/el:19710095. Bibcode: 1971ElL.....7..148H.
- ↑ Grau, G.; Kleen, W. (1982). "Comments on zero-point energy, quantum noise and spontaneous-emission noise". Solid-State Electronics 25 (8): 749–751. doi:10.1016/0038-1101(82)90204-0. Bibcode: 1982SSEle..25..749G.
- ↑ Kleen, W. (1985). "Thermal noise and zero-point-energy". Noise in Physical Systems and 1/F Noise 1985. pp. 331–332. doi:10.1016/B978-0-444-86992-0.50072-2. ISBN 9780444869920. https://archive.org/details/noiseinphysicals00dami.
- ↑ Kiss, L. B. (1988). "To the problem of zero-point energy and thermal noise". Solid State Communications 67 (7): 749–751. doi:10.1016/0038-1098(88)91020-4. Bibcode: 1988SSCom..67..749K.
- ↑ Abbott et al. (1996).
- ↑ Scully (2001).
- ↑ Galve, Fernando; Lutz, Eric (2009). "Nonequilibrium thermodynamic analysis of squeezing". Physical Review A 79 (5): 055804. doi:10.1103/PhysRevA.79.055804. Bibcode: 2009PhRvA..79e5804G.
- ↑ Dillenschneider, R.; Lutz, E. (2009). "Energetics of quantum correlations". EPL 88 (5): 50003. doi:10.1209/0295-5075/88/50003. Bibcode: 2009EL.....8850003D.
- ↑ Huang, X. L.; Wang, Tao; Yi, X. X. (2012). "Effects of reservoir squeezing on quantum systems and work extraction". Physical Review E 86 (5): 051105. doi:10.1103/PhysRevE.86.051105. PMID 23214736. Bibcode: 2012PhRvE..86e1105H.
- ↑ Boukobza, E.; Ritsch, H. (2013). "Breaking the Carnot limit without violating the second law: A thermodynamic analysis of off-resonant quantum light generation". Physical Review A 87 (6): 063845. doi:10.1103/PhysRevA.87.063845. Bibcode: 2013PhRvA..87f3845B.
- ↑ Roßnagel et al. (2014).
- ↑ Correa et al. (2014).
- ↑ Abah, Obinna; Lutz, Eric (2014). "Efficiency of heat engines coupled to nonequilibrium reservoirs". EPL 106 (2): 20001. doi:10.1209/0295-5075/106/20001. Bibcode: 2014EL....10620001A.
- ↑ Gardas, Bartłomiej; Deffner, Sebastian; Saxena, Avadh (2016). "Non-hermitian quantum thermodynamics". Scientific Reports 6: 23408. doi:10.1038/srep23408. PMID 27003686. Bibcode: 2016NatSR...623408G.
- ↑ Gemmer, Jochen; Michel, M.; Mahler, Günter (2009). Quantum Thermodynamics: Emergence of Thermodynamic Behavior Within Composite Quantum Systems. Springer. doi:10.1007/978-3-540-70510-9. ISBN 978-3-540-70510-9. https://cds.cern.ch/record/1339164.
- ↑ Noever, David; Bremner, Christopher (1999). "Large-scale Sakharov condition". AIAA 35th Joint Propulsion Conference and Exhibit. doi:10.2514/6.1999-2146.
- ↑ Haisch, B.; Rueda, A.; Dobyns, Y. (2001). "Inertial mass and the quantum vacuum fields". Annalen der Physik 10 (5): 393–414. doi:10.1002/1521-3889(200105)10:5<393::AID-ANDP393>3.0.CO;2-Z. Bibcode: 2001AnP...513..393H. http://www.calphysics.org/articles/annalen.pdf.
- ↑ Podkletnov, Evgeny; Modanese, Giovanni (2001). "Impulse Gravity Generator Based on Charged YBa2Cu3O7−y Superconductor with Composite Crystal Structure". arXiv:physics/0108005.
- ↑ Matthews, Robert (21 September 1996). "Antigravity machine weighed down by controversy". New Scientist. https://www.newscientist.com/article/mg15120480-800-antigravity-machine-weighed-down-by-controversy/. Retrieved 26 October 2016.
- ↑ Lano, R. P. (1996). "Gravitational Meissner Effect". arXiv:hep-th/9603077.
- ↑ Forward, R. L. (1963). "Guidelines to Antigravity". American Journal of Physics 31 (3): 166–170. doi:10.1119/1.1969340. Bibcode: 1963AmJPh..31..166F. http://u2.lege.net/culture.zapto.org_82_20080124/Om%20nya%20energik%E4llor/Energy%20papers%20%20%20%20Mina%20dokument/antigravidity/guide%20to%20antigravity.pdf.
- ↑ Forward, R. L. (1961). "General Relativity for the Experimentalist". Proceedings of the IRE 49 (5): 892–904. doi:10.1109/JRPROC.1961.287932. Bibcode: 1961PIRE...49..892F.
- ↑ Swain, John (2010). "Gravitatomagnetic Analogs of Electric Transformers". arXiv:1006.5754 [gr-qc].
- ↑ "Physicist Predicts Gravitational Analogue Of Electrical Transformers". MIT Technology Review. 6 July 2010. https://www.technologyreview.com/s/419695/physicist-predicts-gravitational-analogue-of-electrical-transformers/.
- ↑ DeWitt, Bryce S. (1966). "Superconductors and Gravitational Drag". Physical Review Letters 16 (24): 1092–1093. doi:10.1103/PhysRevLett.16.1092. Bibcode: 1966PhRvL..16.1092D.
- ↑ Ross, D. K. (1983). "The London equations for superconductors in a gravitational field". Journal of Physics A 16 (6): 1331–1335. doi:10.1088/0305-4470/16/6/026. Bibcode: 1983JPhA...16.1331R.
- ↑ U.S. Patent 3,626,606
- ↑ U.S. Patent 3,626,605
- ↑ U.S. Patent 3,823,570
- ↑ Barker, B. M.; O'Connell, R. F. (1979). "The gravitational interaction: Spin, rotation, and quantum effects-a review". General Relativity and Gravitation 11 (2): 149–175. doi:10.1007/BF00756587. Bibcode: 1979GReGr..11..149B.
- ↑ O'Connell, R. F. (1970). "The gravitational field of the electron". Physics Letters A 32 (6): 402–403. doi:10.1016/0375-9601(70)90022-8. Bibcode: 1970PhLA...32..402O.
- ↑ O'Connell, R. F.; Rasband, S. N. (1971). "Lense-Thirring Type Gravitational Forces Between Disks and Cylinders". Nature 232 (35): 193–195. doi:10.1038/physci232193a0. Bibcode: 1971NPhS..232..193O.
- ↑ Peres, Asher (1978). "Test of equivalence principle for particles with spin". Physical Review D 18 (8): 2739–2740. doi:10.1103/PhysRevD.18.2739. Bibcode: 1978PhRvD..18.2739P.
- ↑ Obukhov, Yuri N. (2001). "Spin, gravity, and inertia". Physical Review Letters 86 (2): 192–195. doi:10.1103/PhysRevLett.86.192. PMID 11177789. Bibcode: 2001PhRvL..86..192O.
- ↑ Ritter, R. C.; Winkler, L. I.; Gillies, G. T. (1993). "Search for anomalous spin-dependent forces with a polarized-mass torsion pendulum". Physical Review Letters 70 (6): 701–704. doi:10.1103/PhysRevLett.70.701. PMID 10054182. Bibcode: 1993PhRvL..70..701R.
- ↑ "Antigravity Not So Crazy After All". New Scientist 85 (1194): 485. 14 February 1980. https://books.google.com/books?id=2yIbfsnnnVgC.
- ↑ Cravens, D. L. (1990). "Electric Propulsion Study: Final Report". Contract F04611-88-C-0014, Astronautics Laboratory (AFSC), Air Force Space Technology Center, Space Systems Division, Air Force Systems Command, Edwards AFB, CA. http://apps.dtic.mil/dtic/tr/fulltext/u2/a227121.pdf. Retrieved 26 October 2016.
- ↑ Allen, J. E. (2005). "Aeronautics-1903; aerospace-2003; ? ? 2103". Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering 219 (3): 235–260. doi:10.1243/095441005X30252.
- ↑ Thorne, Kip; Michael Morris; Ulvi Yurtsever (1988). "Wormholes, Time Machines, and the Weak Energy Condition". Physical Review Letters 61 (13): 1446–1449. doi:10.1103/PhysRevLett.61.1446. PMID 10038800. Bibcode: 1988PhRvL..61.1446M. http://authors.library.caltech.edu/9262/1/MORprl88.pdf.
- ↑ Wheeler, J Craig (2007). Cosmic Catastrophes (2nd ed.). New York: Cambridge University Press. p. 228. ISBN 978-0521857147. https://archive.org/details/cosmiccatastroph0000whee.
- ↑ Alcubierre, Miguel (1994). "The warp drive: hyper-fast travel within general relativity". Classical and Quantum Gravity 11 (5): L73–L77. doi:10.1088/0264-9381/11/5/001. Bibcode: 1994CQGra..11L..73A.
- ↑ Podkletnov, E.; Nieminen, R. (1992). "A possibility of gravitational force shielding by bulk YBa2Cu3O7−x superconductor". Physica C: Superconductivity 203 (3–4): 441–444. doi:10.1016/0921-4534(92)90055-H. Bibcode: 1992PhyC..203..441P.
- ↑ Rounds, Frederic N. (1998). "Anomalous Weight Behavior in YBa2Cu3O7 Compounds at Low Temperature". Proc. NASA Breakthrough Propulsion Phys. Workshop 279: physics/9705043. Bibcode: 1997physics...5043R.
- ↑ Woods et al. (2001).
- ↑ Tajmar, M.; Plesescu, F.; Marhold, K. & de Matos, C.J. (2006). "Experimental Detection of the Gravitomagnetic London Moment". arXiv:gr-qc/0603033v1.
- ↑ Robertson, Glen A. (1999). "On the Mechanism for a Gravity Effect using Type II Superconductors". NASA Technical Reports Server. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19990046249.pdf. Retrieved 26 October 2016.
- ↑ Li, N.; Torr, D. G. (1991). "Effects of a gravitomagnetic field on pure superconductors". Physical Review D 43 (2): 457–459. doi:10.1103/PhysRevD.43.457. PMID 10013404. Bibcode: 1991PhRvD..43..457L.
- ↑ Li, Ning; Torr, D. G. (1992). "Gravitational effects on the magnetic attenuation of superconductors". Physical Review B 46 (9): 5489–5495. doi:10.1103/PhysRevB.46.5489. PMID 10004334. Bibcode: 1992PhRvB..46.5489L.
- ↑ Torr, Douglas G.; Li, Ning (1993). "Gravitoelectric-electric coupling via superconductivity". Foundations of Physics Letters 6 (4): 371–383. doi:10.1007/BF00665654. Bibcode: 1993FoPhL...6..371T.
- ↑ Kowitt (1994).
- ↑ Harris, Edward G. (1999). "Comments on "Gravitoelectric-Electric Coupling via Superconductivity" by Douglas G. Torr and Ning Li". Foundations of Physics Letters 12 (2): 201–208. doi:10.1023/A:1021621425670.
- ↑ Woods (2005).
- ↑ Tajmar, Martin; de Matos, Clovis (2006). "Gravitomagnetic Fields in Rotating Superconductors to Solve Tate's Cooper Pair Mass Anomaly". AIP Conf. Proc. 813: 1415–1420. doi:10.1063/1.2169327. Bibcode: 2006AIPC..813.1415T. https://cds.cern.ch/record/973877/files/0607086.pdf.
- ↑ Li, N.; Noever, D.; Robertson, T.; Koczor, R.; Brantley, W. (August 1997). "Static Test for a Gravitational Force Coupled to Type II YBCO Superconductors". Physica C 281 (2–3): 260–267. doi:10.1016/S0921-4534(97)01462-7. Bibcode: 1997PhyC..281..260L.
- ↑ Lucentini (2000).
- ↑ "Annual Report on Cooperative Agreements and Other Transactions Entered into During FY2001 Under 10 USC 2371". DOD. p. 66. http://www.acq.osd.mil/dpap/Docs/FY01RPT.doc.
- ↑ Cook (2002).
- ↑ Froning, H.; Roach, R. (2002). "Preliminary Simulations of Vehicle Interactions with the Quantum Vacuum by Fluid Dynamic Approximations". pp. 52236. doi:10.2514/6.2002-3925. ISBN 978-1-62410-115-1.
- ↑ Fontana, Giorgio; Binder, Bernd (2009-03-16). "Electromagnetic to Gravitational wave Conversion via Nuclear Holonomy". AIP Conference Proceedings 1103 (1): 524–531. doi:10.1063/1.3115561. ISSN 0094-243X. Bibcode: 2009AIPC.1103..524F. https://aip.scitation.org/doi/abs/10.1063/1.3115561.
- ↑ Pauling, Linus (October 1965). "The Close-Packed-Spheron Model of Atomic Nuclei and ITS Relation to the Shell Model" (in en). Proceedings of the National Academy of Sciences 54 (4): 989–994. doi:10.1073/pnas.54.4.989. ISSN 0027-8424. PMID 16578621. Bibcode: 1965PNAS...54..989P.
- ↑ White, March, Williams et al. (2011).
- ↑ Maxey, Kyle (11 December 2012). "Propulsion on an Interstellar Scale – the Quantum Vacuum Plasma Thruster". http://www.engineering.com/DesignerEdge/DesignerEdgeArticles/ArticleID/5058/Propulsion-on-an-Interstellar-Scale-the-Quantum-Vacuum-Plasma-Thruster.aspx.
- ↑ Hambling, David (31 July 2014). "Nasa validates 'impossible' space drive". Wired UK. https://www.wired.co.uk/article/nasa-validates-impossible-space-drive. Retrieved 24 October 2016.
- ↑ White, March, Lawrence et al. (2016).
- ↑ Drake, Nadia; Greshko, Michael (21 November 2016). "NASA Team Claims 'Impossible' Space Engine Works—Get the Facts". National Geographic. http://news.nationalgeographic.com/2016/11/nasa-impossible-emdrive-physics-peer-review-space-science/. Retrieved 22 November 2016.
Articles in the press
- Battersby, S. (20 November 2008). "It's Confirmed: Matter is Merely Vacuum Fluctuations". New Scientist. https://www.newscientist.com/article/dn16095-its-confirmed-matter-is-merely-vacuum-fluctuations/.
- Bennett, J. (30 November 2016). "Scientists Catch "Virtual Particles" Hopping In and Out of Existence". http://www.popularmechanics.com/space/a24076/neutron-star-particles-spring-into-existence/.
- Cho, A. (1 October 2015). "Physicists Observe Weird Quantum Fluctuations Of Empty Space—Maybe". Science. doi:10.1126/science.aad4655. https://www.science.org/content/article/physicists-observe-weird-quantum-fluctuations-empty-space-maybe.
- Cho, A. (30 November 2016). "Astronomers Spot Signs of Weird Quantum Distortion in Space". Science. doi:10.1126/science.aal0437. https://www.science.org/content/article/astronomers-spot-signs-weird-quantum-distortion-space.
- Choi, C. Q. (12 February 2013). "Something from Nothing? A Vacuum Can Yield Flashes of Light". https://www.scientificamerican.com/article/something-from-nothing-vacuum-can-yield-flashes-of-light/.
- Chown, M. (7 April 1990). "Science: Can Photons Travel 'Faster Than Light'?". New Scientist. https://www.newscientist.com/article/mg12617112-900-science-can-photons-travel-faster-than-light/.
- Cook, N. (29 July 2002). "Anti-Gravity Propulsion Comes "Out of the Closet"". London. http://www.janes.com/aerospace/civil/news/jdw/jdw020729_1_n.shtml.
- Crane, L. (30 November 2016). "Quantum Particles Seen Distorting Light From a Neutron Star". New Scientist. https://www.newscientist.com/article/2114797-quantum-particles-seen-distorting-light-from-a-neutron-star/#link_time=1480530002.
- Davies, P. C. W. (22 September 1994). "Inertia Theory: Magic Roundabout. Paul Davies on the Meaning of Mach's Principle". The Guardian. http://www.physics.adelaide.edu.au:80/itp/staff/pcwd/Guardian/1994/940922Mach.html.
- Davies, P. C. W. (19 November 2011). "Out of the Ether: The Changing Face of the Vacuum". New Scientist 212 (2839): 50–52. doi:10.1016/S0262-4079(11)62858-3. Bibcode: 2011NewSc.212Q..50D.
- Lucentini, J. (28 September 2000). "Weighty Implications: NASA Funds Controversial Gravity Shield". http://www.space.com/businesstechnology/technology/anti_grav_000928.html.
- Matthews, R. (25 February 1995). "Nothing Like a Vacuum". New Scientist 145 (1966): 30–33. https://www.newscientist.com/article/mg14519664-100-nothing-like-a-vacuum/. Via Calphysics Institute.
- O'Carroll, E. (25 March 2013). "Scientists Examine Nothing, Find Something". http://www.csmonitor.com/Science/2013/0325/Scientists-examine-nothing-find-something.
- Pilkington, M. (17 July 2003). "Zero Point Energy". https://www.theguardian.com/education/2003/jul/17/research.highereducation.
- Powell, C. S. (1994). "Unbearable Lightness: A New Theory May Explain Why Objects Tend to Stay Put". Scientific American 270 (5): 30–31. doi:10.1038/scientificamerican0594-27.
- Scott, W. B. (March 2004). "To the Stars". Aviation Week & Space Technology: 50–53. http://www.zpower.com/en/documents/Paper_ToTheStars.pdf. Retrieved 25 October 2016.
- Siegel, E. (22 September 2016). "What Is The Physics Of Nothing?". https://www.forbes.com/sites/startswithabang/2016/09/22/what-is-the-physics-of-nothing/#423602bc1451.
- Shiga, D. (28 September 2005). "Vacuum Energy: Something For Nothing?". New Scientist. https://www.newscientist.com/article/mg18825191-800-vacuum-energy-something-for-nothing/.
- Wall, M. (27 March 2014). "Does Dark Energy Spring From the 'Quantum Vacuum?'". http://www.space.com/25238-dark-energy-quantum-vacuum-theory.html.
Bibliography
- Abbott, D.; Davis, B. R.; Phillips, N. J.; Eshraghian, K. (1996). "Simple derivation of the thermal noise formula using window-limited Fourier transforms and other conundrums". IEEE Transactions on Education 39 (1): 1–13. doi:10.1109/13.485226. Bibcode: 1996ITEdu..39....1A.
- Barton, G.; Scharnhorst, K. (1993). "QED Between Parallel Mirrors: Light Signals Faster Than c, or Amplified by the Vacuum". Journal of Physics A: Mathematical and General 26 (8): 2037–2046. doi:10.1088/0305-4470/26/8/024. ISSN 0305-4470. Bibcode: 1993JPhA...26.2037B.
- Battersby, Stephen (2016). "Dark energy: Staring into darkness". Nature 537 (7622): 201–204. doi:10.1038/537S201a. PMID 27681049. Bibcode: 2016Natur.537S.201B.
- Bordag, M; Klimchitskaya, G. L.; Mohideen, U.; Mostepanenko, V. M. (2009). Advances in the Casimir Effect. Oxford: Oxford University Press. ISBN 978-0-19-923874-3. OCLC 319209483. https://books.google.com/books?id=CqE1f_s5PgYC.
- Bostick, W. H.; Prior, W.; Grunberger, L.; Emmert, G. (1966). "Pair Production of Plasma Vortices". Physics of Fluids 9 (10): 2078. doi:10.1063/1.1761572. Bibcode: 1966PhFl....9.2078B.
- Bressi, G.; Carugno, G.; Onofrio, R.; Ruoso, G. (2002). "Measurement of the Casimir Force between Parallel Metallic Surfaces". Physical Review Letters 88 (4): 041804. doi:10.1103/PhysRevLett.88.041804. PMID 11801108. Bibcode: 2002PhRvL..88d1804B.
- Capasso, F.; Munday, J. N.; Iannuzzi, D.; Chan, H. B. (2007). "Casimir Forces and Quantum Electrodynamical Torques: Physics and Nanomechanics". IEEE Journal of Selected Topics in Quantum Electronics 13 (2): 400–414. doi:10.1109/JSTQE.2007.893082. Bibcode: 2007IJSTQ..13..400C. http://www.seas.harvard.edu/capasso/wp-content/uploads/publications/Capasso_STJQE_13_400_2007.pdf.
- Carroll, S. M.; Field, G. B. (1997). "Is There Evidence for Cosmic Anisotropy in the Polarization of Distant Radio Sources?". Physical Review Letters 79 (13): 2394–2397. doi:10.1103/PhysRevLett.79.2394. ISSN 0031-9007. Bibcode: 1997PhRvL..79.2394C. https://cds.cern.ch/record/324872/files/9704263.pdf.
- Chan, H. B.; Aksyuk, V. A.; Kleiman, R. N.; Bishop, D. J.; Capasso, F. (2001). "Quantum Mechanical Actuation of Microelectromechanical Systems by the Casimir Force". Science 291 (5510): 1941–1944. doi:10.1126/science.1057984. PMID 11239149. Bibcode: 2001Sci...291.1941C. https://www.mit.edu/~kardar/research/seminars/Casimir/Science-Capasso.pdf.
- Conlon, T. E. (2011). Thinking About Nothing : Otto Von Guericke and The Magdeburg Experiments on the Vacuum. San Francisco: Saint Austin Press. ISBN 978-1-4478-3916-3. OCLC 840927124. https://books.google.com/books?id=rL9jAwAAQBAJ.
- Correa, L. A.; Palao, J. P.; Alonso, D.; Adesso, G. (2014). "Quantum-enhanced absorption refrigerators". Scientific Reports 4 (3949): 3949. doi:10.1038/srep03949. PMID 24492860. Bibcode: 2014NatSR...4E3949C.
- Davies, P. C. W. (1985). Superforce: The Search for a Grand Unified Theory of Nature. New York: Simon and Schuster. ISBN 978-0-671-47685-4. OCLC 12397205. https://archive.org/details/superforcesearch00davi.
- Decca, R. S.; López, D.; Fischbach, E.; Krause, D. E. (2003). "Measurement of the Casimir Force between Dissimilar Metals". Physical Review Letters 91 (5): 050402. doi:10.1103/PhysRevLett.91.050402. PMID 12906584. Bibcode: 2003PhRvL..91e0402D. http://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=2101&context=physics_articles.
- Dirac, Paul A. M. (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proc. R. Soc. A 114 (767): 243–265. doi:10.1098/rspa.1927.0039. Bibcode: 1927RSPSA.114..243D. http://www.imotiro.org/repositorio/howto/artigoshistoricosordemcronologica/1927%20-%20DIRAC%201927%20First%20steps%20in%20quantum%20field%20theory%20Invention%20of%20the%20second%20quantization%20method.pdf. Retrieved 17 October 2016.
- Drexhage, K. H. (1970). "Monomolecular Layers and Light". Scientific American 222 (3): 108–119. doi:10.1038/scientificamerican0370-108. Bibcode: 1970SciAm.222c.108D.
- Drexhage, K. H. (1974). "IV Interaction of Light with Monomolecular Dye Layers". in Wolf, E.. Progress in Optics. 12. pp. 163–232. doi:10.1016/S0079-6638(08)70266-X. ISBN 978-0-444-10571-4.
- Dunne, G. V. (2012). "The Heisenberg-Euler Effective Action: 75 years on". International Journal of Modern Physics A 27 (15): 1260004. doi:10.1142/S0217751X12600044. ISSN 0217-751X. Bibcode: 2012IJMPA..2760004D.
- Einstein, A. (1995). Klein, Martin J.; Kox, A. J.; Renn, Jürgen et al.. eds. The Collected Papers of Albert Einstein Vol. 4 The Swiss Years: Writings, 1912–1914. Princeton: Princeton University Press. ISBN 978-0-691-03705-9. OCLC 929349643. http://einsteinpapers.press.princeton.edu/vol4-doc/.
- Einstein, A. (1993). Klein, Martin J.; Kox, A. J.; Schulmann, Robert. eds. The Collected Papers of Albert Einstein Vol. 5 The Swiss Years: Correspondence, 1902–1914. Princeton: Princeton University Press. ISBN 978-0-691-03322-8. OCLC 921496342. https://einsteinpapers.press.princeton.edu/vol5-doc/.
- Goy, P.; Raimond, J. M.; Gross, M.; Haroche, S. (1983). "Observation of Cavity-Enhanced Single-Atom Spontaneous Emission". Physical Review Letters 50 (24): 1903–1906. doi:10.1103/PhysRevLett.50.1903. Bibcode: 1983PhRvL..50.1903G.
- Greiner, W.; Müller, B.; Rafelski, J. (2012). Quantum Electrodynamics of Strong Fields: With an Introduction into Modern Relativistic Quantum Mechanics. Springer. doi:10.1007/978-3-642-82272-8. ISBN 978-0-387-13404-8. OCLC 317097176. https://books.google.com/books?id=Wh3-CAAAQBAJ.
- Haisch, B.; Rueda, A.; Puthoff, H. E. (1994). "Inertia as a Zero-Point-Field Lorentz Force". Physical Review A 49 (2): 678–694. doi:10.1103/PhysRevA.49.678. PMID 9910287. Bibcode: 1994PhRvA..49..678H. http://www.zpower.com/sp/documents/ZPEPaper_InertiaAsAZeroPointFieldLorenzForce.pdf. Retrieved 17 October 2016.
- Heisenberg, W.; Euler, H. (1936). "Folgerungen aus der Diracschen Theorie des Positrons". Zeitschrift für Physik 98 (11–12): 714–732. doi:10.1007/BF01343663. ISSN 1434-6001. Bibcode: 1936ZPhy...98..714H.
- Heyl, J. S.; Shaviv, N. J. (2000). "Polarization evolution in strong magnetic fields". Monthly Notices of the Royal Astronomical Society 311 (3): 555–564. doi:10.1046/j.1365-8711.2000.03076.x. ISSN 0035-8711. Bibcode: 2000MNRAS.311..555H.
- Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory (2005 ed.). Mineola, New York: Dover Publications. ISBN 978-0486445687. OCLC 61200849. https://books.google.com/books?id=4MwsAwAAQBAJ.
- Kostelecký, V. Alan; Mewes, M. (2009). "Electrodynamics with Lorentz-violating operators of arbitrary dimension". Physical Review D 80 (1): 015020. doi:10.1103/PhysRevD.80.015020. ISSN 1550-7998. Bibcode: 2009PhRvD..80a5020K.
- Kostelecký, V. Alan; Mewes, M. (2013). "Constraints on Relativity Violations from Gamma-Ray Bursts". Physical Review Letters 110 (20): 201601. doi:10.1103/PhysRevLett.110.201601. ISSN 0031-9007. PMID 25167393. Bibcode: 2013PhRvL.110t1601K.
- Kowitt, Mark (1994). "Gravitomagnetism and magnetic permeability in superconductors". Physical Review B 49 (1): 704–708. doi:10.1103/PhysRevB.49.704. PMID 10009347. Bibcode: 1994PhRvB..49..704K.
- Kragh, H. (2002). Quantum Generations: A History of Physics in the Twentieth Century. Princeton University Press. ISBN 978-0-691-09552-3. OCLC 248763258.
- Kragh, H. (2012). "Preludes to Dark Energy: Zero-Point Energy and Vacuum Speculations". Archive for History of Exact Sciences 66 (3): 199–240. doi:10.1007/s00407-011-0092-3. ISSN 0003-9519.
- Kragh, H. S.; Overduin, J. M. (2014). The Weight of the Vacuum : A Scientific History of Dark Energy. New York: Springer. ISBN 978-3-642-55089-8. OCLC 884863929. https://books.google.com/books?id=sroqBAAAQBAJ.
- Kuhn, T. (1978). Black-Body Theory and the Quantum Discontinuity, 1894-1912. New York: Oxford University Press. ISBN 978-0-19-502383-1. OCLC 803538583.
- Le Bellac, M. (2006). Quantum Physics (2012 ed.). Cambridge University Press. ISBN 978-1-107-60276-2. OCLC 957316740.
- Leuchs, G.; Sánchez-Soto, L. L. (2013). "A Sum Rule For Charged Elementary Particles". The European Physical Journal D 67 (3): 57. doi:10.1140/epjd/e2013-30577-8. ISSN 1434-6060. Bibcode: 2013EPJD...67...57L.
- Loudon, R. (2000). The Quantum Theory of Light (3rd ed.). Oxford: Oxford University Press. ISBN 978-0198501770. OCLC 44602993. https://books.google.com/books?id=AEkfajgqldoC.
- Matthews, R. (1994). "Inertia: Does Empty Space Put Up the Resistance?". Science 263 (5147): 612–613. doi:10.1126/science.263.5147.612. ISSN 0036-8075. PMID 17747645. Bibcode: 1994Sci...263..612M. http://www.calphysics.org/haisch/science.html.
- Mignani, R. P.; Testa, V.; González Caniulef, D.; Taverna, R.; Turolla, R.; Zane, S.; Wu, K. (2017). "Evidence for vacuum birefringence from the first optical-polarimetry measurement of the isolated neutron star RX J1856.5−3754". Monthly Notices of the Royal Astronomical Society 465 (1): 492–500. doi:10.1093/mnras/stw2798. ISSN 0035-8711. Bibcode: 2017MNRAS.465..492M. https://www.eso.org/public/archives/releases/sciencepapers/eso1641/eso1641a.pdf.
- Milonni, P. W. (1981). "Radiation reaction and the nonrelativistic theory of the electron". Physics Letters A 82 (5): 225–226. doi:10.1016/0375-9601(81)90191-2. Bibcode: 1981PhLA...82..225M.
- Milonni, P. W. (1983). "Does the Electromagnetic Mass of an Electron Depend on Where It Is?". International Journal of Theoretical Physics 22 (4): 323–328. doi:10.1007/BF02082897. Bibcode: 1983IJTP...22..323M.
- Milonni, P. W. (1994). The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Boston: Academic Press. ISBN 978-0124980808. OCLC 422797902.
- Milonni, P. W. (2009). "Zero-Point Energy". in Greenberger, D.; Hentschel, K.; Weinert, F.. Compendium of Quantum Physics: Concepts, Experiments, History and Philosophy. Berlin, Heidelberg: Springer. pp. 864–866. doi:10.1007/978-3-540-70626-7. ISBN 9783540706229. OCLC 297803628. https://books.google.com/books?id=ekyAV8VtfuYC&pg=PP864.
- Peebles, P. J. E.; Ratra, Bharat (2003). "The Cosmological Constant and Dark Energy". Reviews of Modern Physics 75 (2): 559–606. doi:10.1103/RevModPhys.75.559. ISSN 0034-6861. Bibcode: 2003RvMP...75..559P.
- Penrose, Roger (2004). The Road to Reality (8th ed.). New York: Alfred A. Knopf. ISBN 978-0-679-45443-4. OCLC 474890537. https://archive.org/details/roadtorealitycom00penr_0.
- Perlmutter, S.; Aldering; Goldhaber; Knop; Nugent; Castro; Deustua; Fabbro et al. (1999). "Measurements of Ω and Λ from 42 High-Redshift Supernovae". Astrophysical Journal 517 (2): 565–86. doi:10.1086/307221. Bibcode: 1999ApJ...517..565P.
- Peskin, M. E.; Schroeder, D. V. (1995). An Introduction To Quantum Field Theory. Addison-Wesley. ISBN 978-0-201-50397-5. OCLC 635667163. https://archive.org/details/introductiontoqu0000pesk.
- Pinto, F. (1999). "Engine cycle of an optically controlled vacuum energy transducer". Physical Review B 60 (21): 14740. doi:10.1103/PhysRevB.60.14740. Bibcode: 1999PhRvB..6014740P.
- Planck, M. (1900). "Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum". Verhandlungen der Deutschen Physikalischen Gesellschaft 2: 237–245.
- Planck, M. (1911). "Eine neue Strahlungshypothese". Verhandlungen der Deutschen Physikalischen Gesellschaft 13: 138–148.
- Planck, M. (1912a). "Über die Begründung das Gesetzes des schwarzen Strahlung". Annalen der Physik 37 (4): 642–656. doi:10.1002/andp.19123420403. Bibcode: 1912AnP...342..642P. https://zenodo.org/record/1424227.
- Planck, M. (1912b). "La loi du rayonnement noir et l'hypothèse des quantités élémentaires d'action". in Langevin, P.; Solvay, E.; de Broglie, M.. La Théorie du Rayonnement et les Quanta. Paris: Gauthier-Villars. pp. 93–114. OCLC 5894537227. https://archive.org/details/lathoriedurayo00inst.
- Planck, M. (1913). Vorlesungen über die Theorie der Wärmestrahlung. Leipzig: J. A. Barth. OCLC 924400975. https://archive.org/details/bub_gb_k21KAAAAMAAJ.
- Planck, M. (1958). Physikalische Abhandlungen und Vorträge. Vol. 2. Braunschweig: Vieweg & Sohn. OCLC 603096370.
- Power, E. A. (1964). Introductory Quantum Electrodynamics. London: Longmans. OCLC 490279969.
- Reed, D. (1995). "Foundational Electrodynamics and Beltrami Vector Fields". in Barrett, Terence William; Grimes, Dale M.. Advanced Electromagnetism: Foundations, Theory and Applications. Singapore: World Scientific. pp. 217–249. ISBN 978-981-02-2095-2. https://books.google.com/books?id=OdnsCgAAQBAJ&pg=PA217.
- Rees, Martin, ed (2012). Universe. New York: DK Pub. ISBN 978-0-7566-9841-6. OCLC 851193468. https://books.google.com/books?id=IvDZqZz0Q-QC.
- Riek, C.; Seletskiy, D. V.; Moskalenko, A. S.; Schmidt, J. F.; Krauspe, P.; Eckart, S.; Eggert, S.; Burkard, G. et al. (2015). "Direct Sampling of Electric-Field Vacuum Fluctuations". Science 350 (6259): 420–423. doi:10.1126/science.aac9788. ISSN 0036-8075. PMID 26429882. Bibcode: 2015Sci...350..420R. http://kops.uni-konstanz.de/bitstream/handle/123456789/31877/Leitensdorfer_0-301750.pdf?sequence=1&isAllowed=y.
- Riess, A. G.; Filippenko; Challis; Clocchiatti; Diercks; Garnavich; Gilliland; Hogan et al. (1998). "Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant". Astronomical Journal 116 (3): 1009–38. doi:10.1086/300499. Bibcode: 1998AJ....116.1009R.
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. (2014). "Nanoscale Heat Engine Beyond the Carnot Limit". Physical Review Letters 112 (3): 030602. doi:10.1103/PhysRevLett.112.030602. PMID 24484127. Bibcode: 2014PhRvL.112c0602R.
- Rugh, S. E.; Zinkernagel, H. (2002). "The Quantum Vacuum and the Cosmological Constant Problem". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 33 (4): 663–705. doi:10.1016/S1355-2198(02)00033-3. ISSN 1355-2198. Bibcode: 2002SHPMP..33..663R.
- Saunders, Simon; Brown, Harvey R., eds (1991). The Philosophy of Vacuum. Oxford: Oxford University Press. ISBN 978-0198244493. OCLC 774073198.
- Schwinger, J. (1998a). Particles, Sources, and Fields: Volume I. Reading, Massachusetts: Advanced Book Program, Perseus Books. ISBN 978-0-7382-0053-8. OCLC 40544377.
- Schwinger, J. (1998b). Particles, Sources, and Fields: Volume II. Reading, Massachusetts: Advanced Book Program, Perseus Books. ISBN 978-0-7382-0054-5. OCLC 40544377.
- Schwinger, J. (1998c). Particles, Sources, and Fields: Volume III. Reading, Massachusetts: Advanced Book Program, Perseus Books. ISBN 978-0-7382-0055-2. OCLC 40544377.
- Sciama, D. W. (1991). "The Physical Significance of the Vacuum State of a Quantum Field". in Saunders, Simon; Brown, Harvey R.. The Philosophy of Vacuum. Oxford: Oxford University Press. ISBN 978-0198244493. OCLC 774073198.
- Scott, Alwyn (2006). Encyclopedia of Nonlinear Science. Routledge. ISBN 978-1-57958-385-9. OCLC 937249213. https://books.google.com/books?id=KC7gZmIEAiwC.
- Scully, M. O.; Zubairy, M. S. (1997). Quantum optics. Cambridge UK: Cambridge University Press. ISBN 978-0-521-43595-6. OCLC 444869786.
- Scully, M. O. (2001). "Extracting Work from a Single Thermal Bath via Quantum Negentropy". Physical Review Letters 87 (22): 220601. doi:10.1103/PhysRevLett.87.220601. PMID 11736390. Bibcode: 2001PhRvL..87v0601S.
- Scully, M. O.; Zubairy, M. S.; Agarwal, G. S.; Walther, H. (2003). "Extracting Work from a Single Heat Bath via Vanishing Quantum Coherence". Science 299 (5608): 862–863. doi:10.1126/science.1078955. PMID 12511655. Bibcode: 2003Sci...299..862S.
- Urban, M.; Couchot, F.; Sarazin, X.; Djannati-Atai, A. (2013). "The Quantum Vacuum as the Origin of the Speed of Light". The European Physical Journal D 67 (3): 58. doi:10.1140/epjd/e2013-30578-7. ISSN 1434-6060. Bibcode: 2013EPJD...67...58U.
- Weinberg, S. (1989). "The Cosmological Constant Problem". Reviews of Modern Physics 61 (1): 1–23. doi:10.1103/RevModPhys.61.1. ISSN 0034-6861. Bibcode: 1989RvMP...61....1W. https://repositories.lib.utexas.edu/bitstream/2152/61094/1/Weinberg_1989.pdf.
- Weinberg, S. (2015). Lectures on Quantum Mechanics (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-1-107-11166-0. OCLC 910664598.
- Weisskopf, V. (1936). "Über die Elektrodynamik des Vakuums auf Grund des Quantentheorie des Elektrons". Kongelige Danske Videnskabernes Selskab, Mathematisk-fysiske Meddelelse 24 (6): 3–39. http://neo-classical-physics.info/uploads/3/0/6/5/3065888/weisskopf_-_electrodynamics.pdf.
- White, H.; March, P.; Lawrence, J.; Vera, J.; Sylvester, A.; Brady, D.; Bailey, P. (2016). "Measurement of Impulsive Thrust from a Closed Radio-Frequency Cavity in Vacuum". Journal of Propulsion and Power 33 (4): 830–841. doi:10.2514/1.B36120.
- White, H.; March, P.; Williams, N.; O'Neill, W. (2011-12-05). "Eagleworks Laboratories: Advanced Propulsion Physics Research". JANNAF Joint Propulsion Meeting; 5–9 December 2011; Huntsville, AL. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20110023492.pdf. Retrieved 24 October 2016.
- Wilson, C. M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J. R.; Duty, T.; Nori, F.; Delsing, P. (2011). "Observation of the Dynamical Casimir Effect in a Superconducting Circuit". Nature 479 (7373): 376–379. doi:10.1038/nature10561. ISSN 0028-0836. PMID 22094697. Bibcode: 2011Natur.479..376W.
- Woods, R. C. (2005). "Manipulation of gravitational waves for communications applications using superconductors". Physica C: Superconductivity 433 (1–2): 101–107. doi:10.1016/j.physc.2005.10.003. Bibcode: 2005PhyC..433..101W.
- Woods, R. C.; Cooke, S. G.; Helme, J.; Caldwell, C. H. (2001). "Gravity modification by high-temperature superconductors". AIAA 37th Joint Propulsion Conference and Exhibit. doi:10.2514/6.2001-3363.
Further reading
Press articles
- Brumfiel, G. (3 June 2011). "Moving Mirrors Make Light From Nothing". Nature. doi:10.1038/news.2011.346. http://www.nature.com/news/2011/110603/full/news.2011.346.html.
- Brooks, M. (16 November 2011). "Light Pulled Out of Empty Space". New Scientist. https://www.newscientist.com/article/mg21228392-700-light-pulled-out-of-empty-space/.
- Cartlidge, E. (17 November 2011). "How to Turn Darkness into Light". Physics World (Institute of Physics). http://physicsworld.com/cws/article/news/2011/nov/17/how-to-turn-darkness-into-light.
- Marcus, A. (12 October 2009). "Research in a Vacuum: DARPA Tries to Tap Elusive Casimir Effect for Breakthrough Technology". Scientific American. https://www.scientificamerican.com/article/darpa-casimir-effect-research/.
- Matthews, R.; Sample, I. (1 September 1996). "'Anti-Gravity' Device Gives Science a Lift". The Sunday Telegraph. https://www.telegraph.co.uk/htmlContent.jhtml?html=%2Farchive%2F1996%2F09%2F01%2Fngrav01.html.
- Sciama, D. W. (2 Feb 1978). "The Ether Transmogrified". New Scientist 77 (1088): 298–300. https://books.google.com/books?id=5RHTCiRgnB0C&pg=PA298.
- Yirka, B. (2 October 2015). "Research Team Claims to Have Directly Sampled Electric-Field Vacuum Fluctuations". https://phys.org/news/2015-10-team-sampled-electric-field-vacuum-fluctuations.html.
Journal articles
- Boyer, T. H. (1970). "Quantum Zero-Point Energy and Long-Range Forces". Annals of Physics 56 (2): 474–503. doi:10.1016/0003-4916(70)90027-8. ISSN 0003-4916. Bibcode: 1970AnPhy..56..474B.
- Bulsara, A. R.; Gammaitoni, L. (1996). "Tuning in to Noise". Physics Today 49 (3): 39–45. doi:10.1063/1.881491. ISSN 0031-9228. Bibcode: 1996PhT....49c..39B. http://www.nipslab.org/files/vol49no3p39-45.pdf. Retrieved 31 May 2017.
- Lahteenmaki, P.; Paraoanu, G. S.; Hassel, J.; Hakonen, P. J. (2013). "Dynamical Casimir Effect in a Josephson Metamaterial". Proceedings of the National Academy of Sciences 110 (11): 4234–4238. doi:10.1073/pnas.1212705110. ISSN 0027-8424. Bibcode: 2013PNAS..110.4234L.
Books
- Beiser, A. (2003). Concepts of Modern Physics (6th ed.). Boston: McGraw-Hill. ISBN 978-0072448481. OCLC 48965418. https://books.google.com/books?id=34l9CgAAQBAJ.
- Heitler, W. (1984). The Quantum Theory of Radiation (1954 reprint 3rd ed.). New York: Dover Publications. ISBN 978-0486645582. OCLC 924845769. https://books.google.com/books?id=L7w7UpecbKYC.
- Rafelski, J.; Muller, B. (1985). Structured Vacuum: Thinking About Nothing. H. Deutsch: Thun. ISBN 978-3871448898. OCLC 946050522. http://www.physics.arizona.edu/~rafelski/Books/StructVacuumE.pdf.
External links
| Wikimedia Commons has media related to Zero-point energy. |
- Nima Arkani-Hamed on the issue of vacuum energy and dark energy.
- Steven Weinberg on the cosmological constant problem.
 |