Astronomy:Groundwater on Mars

From HandWiki
Short description: Water held in permeable ground
The preservation and cementation of aeolian dune stratigraphy in Burns Cliff in Endurance Crater are thought to have been controlled by flow of shallow groundwater.[1]

Rain and snow was a regular occurrence on Mars in the past; especially in the Noachian and early Hesperian epochs.[2][3][4][5][6][7] Some moisture entered the ground and formed aquifers. That is, the water went into the ground, seeped down until it reached a formation that would not allow it to penetrate further (such a layer is called impermeable). Water then accumulated forming a saturated layer. Deep aquifers may still exist.[8]

Overviews

Researchers have found that Mars had a planet-wide groundwater system and several prominent features on the planet have been produced by the action of groundwater.[9][10] When water rose to the surface or near the surface, various minerals were deposited and sediments became cemented together. Some of the minerals were sulfates that were probably produced when water dissolved sulfur from underground rocks, and then became oxidized when it came into contact with the air.[11][12][13] While traveling through the aquifer, the water passed through igneous rock basalt, which would have contained sulfur.

In an aquifer, water occupies open space (pore space) that lies between rock particles. This layer would spread out, eventually coming to be under most of the Martian surface. The top of this layer is called the water table. Calculations show that the water table on Mars was for a time 600 meters below the surface.[14][15]

The InSight lander uncovered in September 2019 unexplained magnetic pulses, and magnetic oscillations consistent with an existing planet-wide reservoir of liquid water deep underground.[8]

Researchers have concluded that Gale Crater has experienced many episodes of groundwater surge with changes in the groundwater chemistry. These chemical changes would support life.[16][17][18][19][20][21]

Layered terrain

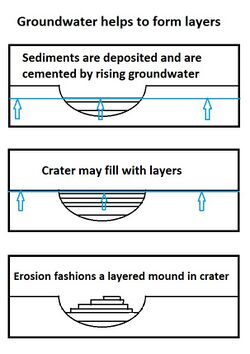
Layers may be formed by groundwater rising up depositing minerals and cementing sediments. The hardened layers are consequently more protected from erosion. This process may occur instead of layers forming under lakes.

Some locations on the Red Planet show groups of layered rocks.[22][23] Rock layers are present under the resistant caps of pedestal craters, on the floors of many large impact craters, and in the area called Arabia.[24][25] In some places the layers are arranged into regular patterns.[26][27] It has been suggested that the layers were put into place by volcanoes, the wind, or by being at the bottom of a lake or sea. Calculations and simulations show that groundwater carrying dissolved minerals would surface in the same locations that have abundant rock layers. According to these ideas, deep canyons and large craters would receive water coming from the ground. Many craters in the Arabia area of Mars contain groups of layers. Some of these layers may have resulted from climate change.

The tilt of the rotational axis of Mars has repeatedly changed in the past. Some changes are large. Because of these variations of climate, at times the atmosphere of Mars would have been much thicker and contained more moisture. The amount of atmospheric dust also has increased and decreased. It is believed that these frequent changes helped to deposit material in craters and other low places. The rising of mineral-rich ground water cemented these materials. The model also predicts that after a crater is full of layered rocks, additional layers will be laid down in the area around the crater. So, the model predicts that layers may also have formed in intercrater regions; layers in these regions have been observed.

Layers can be hardened by the action of groundwater. Martian ground water probably moved hundreds of kilometers, and in the process it dissolved many minerals from the rock it passed through. When ground water surfaces in low areas containing sediments, water evaporates in the thin atmosphere and leaves behind minerals as deposits and/or cementing agents. Consequently, layers of dust could not later easily erode away since they were cemented together. On Earth, mineral-rich waters often evaporate forming large deposits of various types of salts and other minerals. Sometimes water flows through Earth's aquifers, and then evaporates at the surface just as is hypothesized for Mars. One location this occurs on Earth is the Great Artesian Basin of Australia .[28] On Earth the hardness of many sedimentary rocks, like sandstone, is largely due to the cement that was put in place as water passed through.

In February 2019, European scientists published geological evidence of an ancient planet-wide groundwater system that was, arguably, connected to a putative vast ocean.[29][30]

Layers in Crommelin crater

Layers in Danielson crater

  • Layered mound on floor of Danielson crater, as seen by HiRISE under HiWish program

  • Close, color view of layers and dark dust on floor, as seen by HiRISE

  • Close, color view of layers and dark dust on floor, as seen by HiRISE. Boulders are visible in the image.

  • Close view of layers on floor, as seen by HiRISE. Some faults are visible in image.

  • Layers seen by HiRISE. The box represents the size of a football field.

  • Close up of layers as seen by HiRISE. Boulders are visible, as well as dark sand.

Inverted terrain

Many areas on Mars show inverted relief. In those places, former stream channels are displayed as raised beds, instead of stream valleys. Raised beds form when old stream channels become filled with material that is resistant to erosion. After later erosion removes surrounding soft materials, more resistant materials that were deposited in the stream bed are left behind. Lava is one substance that can flow down valleys and produce such inverted terrain. However, fairly loose materials can get quite hard and erosion resistant when cemented by minerals. These minerals can come from groundwater. It is thought that a low point, like a valley focuses groundflow, so more water and cements move into it, and this results in a greater degree of cementation.[9]

Terrain inversion can also happen without cementation by groundwater, however. If a surface is being eroded by wind, the necessary contrast in erodibility can arise simply from variations in grain size of loose sediments. Since wind can carry away sand but not cobbles, for example, a channel bed rich in cobbles could form an inverted ridge if it was originally surrounded by much finer sediments, even if the sediments were not cemented. This effect has been invoked for channels in Saheki crater.[31]

Places on Mars that contain layers in the bottoms of craters often also have inverted terrain.

  • Inverted channel in Miyamoto, as seen by HiRISE. The scale bar is 500 meters long.

  • CTX context image for next image that was taken with HiRISE. Note long ridge going across image is probably an old stream. Box indicates area for HiRISE image. Image located in Margaritifer Sinus quadrangle.

  • Example of inverted terrain in Parana Valles region, as seen by HiRISE.

Evidence for groundwater upwelling

Spacecraft sent to Mars provided a wealth of evidence for groundwater being a major cause of many rock layers on the planet. The Opportunity Rover studied some areas with sophisticated instruments. Opportunity’s observations showed that groundwater repeatedly had risen to the surface. Evidence for water coming to the surface a number of times include hematite concretions (called "blue berries"), cementation of sediments, alteration of sediments, and clasts or skeletons of formed crystals.[32] [33] [34] To produce skeleton crystals, dissolved minerals were deposited as mineral crystals, and then the crystals were dissolved when more water came to the surface at a later time. The shape of the crystals could still be made out.[35] Opportunity found hematite and sulfates in many places as it traveled on the surface of Mars, so it is assumed that the same types of deposits are widespread, just as predicted by the model.[36][37][38][39]

  • Holes (Vugs) in bedrock in the shape of crystals that were there, but have since been dissolved, as seen by Opportunity Rover. The holes have the shape of the original crystals.

"Blueberries" (hematite spheres) on a rocky outcrop at Eagle Crater. Note the merged triplet in the upper left.

Orbiting probes showed that the type of rock around Opportunity was present in a very large area that included Arabia, which is about as large as Europe. A spectroscope, called CRISM, on the Mars Reconnaissance Orbiter found sulfates in many of the same places that the upwelling water model had predicted, including some areas of Arabia.[40] The model predicted deposits in Valles Marineris canyons; these deposits have been observed and found to contain sulfates.[41] Other locations predicted to have upwelling water, for example chaos regions and canyons associated with large outflows, have also been found to contain sulfates.[42][43] Layers occur in the types of locations predicted by this model of groundwater evaporating at the surface. They were discovered by the Mars Global Surveyor and HiRISE onboard Mars Reconnaissance Orbiter. Layers have been observed around the site that Opportunity landed and in nearby Arabia. The ground under the cap of pedestal craters sometimes displays numerous layers. The cap of a pedestal crater protects material under it from eroding away. It is accepted that the material that now is only found under the pedestal crater’s cap formerly covered the whole region. Hence, layers now just visible under pedestal craters once covered the whole area. Some craters contain mounds of layered material that reach above the crater’s rim. Gale Crater and Crommelin (Martian crater) are two craters that hold large mounds. Such tall mounds were formed, according to this model, by layers that first filled the crater, and then continued to build up around the surrounding region. Later erosion removed material around the crater, but left a mound in the crater that was higher than its rim. Note that although the model predicts upwelling and evaporation that should have produced layers in other areas (Northern lowlands), these areas do not show layers because the layers were formed long ago in the Early Hesperian Epoch and were therefore subsequently buried by later deposits.

Strong evidence for groundwater making lakes in deep craters was described by a group of European scientists in February 2019.[29][30][44][45] Craters examined did not show inlets or outlets; therefore, water for the lake would have come from the ground. These craters had floors lying roughly 4000 m below Martian 'sea level'. Features and minerals on the floors of these craters could only have formed in the presence of water. Some of the features were deltas and terraces.[46][44] Some of the craters studied were Oyama, Pettit, Sagan, Tombaugh, Mclaughlin, du Martheray, Nicholson, Curie, and Wahoo. It seems that if a crater was deep enough, water came out of the ground and a lake was formed.[44]

Pedestal craters

  • Tikhonravov crater floor with two pedestal craters, as seen by Mars Global Surveyor. Image in Arabia quadrangle.

  • Dark slope streaks and layers near the top of a pedestal crater, as seen by HiRISE. Image in Arabia quadrangle.

  • Pedestal craters form when the ejecta from impacts protect the underlying material from erosion. As a result of this process, craters appear perched above their surroundings.

  • Dark slope streaks and layers near a pedestal crater, as seen by HiRISE. Layers were protected by the top of the pedestal crater. Image in Arabia quadrangle.

See also


References

  1. ↑ Grotzinger, J.P.; Arvidson, R.E.; Bell, III; Calvin, W.; Clark, B.C.; Fike, D.A.; Golombek, M.; Greeley, R. et al. (2005). "Stratigraphy and sedimentology of a dry to wet eolian depositional system, Burns formation, Meridiani Planum, Mars". Earth and Planetary Science Letters 240 (1): 11–72. doi:10.1016/j.epsl.2005.09.039. Bibcode: 2005E&PSL.240...11G. 
  2. ↑ Carr, Michael H. (1995). "The Martian drainage system and the origin of valley networks and fretted channels". Journal of Geophysical Research 100 (E4): 7479–7507. doi:10.1029/95JE00260. Bibcode: 1995JGR...100.7479C. https://zenodo.org/record/1231366. 
  3. ↑ Carr, Michael H.; Chuang, Frank C. (1997). "Martian drainage densities". Journal of Geophysical Research 102 (E4): 9145–9152. doi:10.1029/97JE00113. Bibcode: 1997JGR...102.9145C. 
  4. ↑ Baker, V. R. (1982), The Channels of Mars, 198 pp., Univ. of Tex. Press, Austin.
  5. ↑ Barnhart, Charles J.; Howard, Alan D.; Moore, Jeffrey M. (2009). "Long-term precipitation and late-stage valley network formation: Landform simulations of Parana Basin, Mars". Journal of Geophysical Research 114 (E1): E01003. doi:10.1029/2008JE003122. Bibcode: 2009JGRE..114.1003B. 
  6. ↑ Howard, Alan D.; Moore, Jeffrey M.; Irwin, Rossman P. (2005). "An intense terminal epoch of widespread fluvial activity on early Mars: 1. Valley network incision and associated deposits". Journal of Geophysical Research 110 (E12): E12S14. doi:10.1029/2005JE002459. Bibcode: 2005JGRE..11012S14H. 
  7. ↑ Stepinski, T. F.; Stepinski, A. P. (2005). "Morphology of drainage basins as an indicator of climate on early Mars". Journal of Geophysical Research 110 (E12): E12S12. doi:10.1029/2005JE002448. Bibcode: 2005JGRE..11012S12S. 
  8. ↑ 8.0 8.1 Andrews, Robin George (20 September 2019). "Mysterious magnetic pulses discovered on Mars - The nighttime events are among initial results from the InSight lander, which also found hints that the red planet may host a global reservoir of liquid water deep below the surface.". National Geographic Society. https://www.nationalgeographic.com/science/2019/09/mars-insight-feels-mysterious-magnetic-pulsations-at-midnight/. 
  9. ↑ 9.0 9.1 Andrews-Hanna, Jeffrey C.; Phillips, Roger J.; Zuber, Maria T. (2007). "Meridiani Planum and the global hydrology of Mars". Nature 446 (7132): 163–6. doi:10.1038/nature05594. PMID 17344848. Bibcode: 2007Natur.446..163A. 
  10. ↑ Salese, Francesco; Pondrelli, Monica; Neeseman, Alicia; Schmidt, Gene; Ori, Gian Gabriele (2019). "Geological Evidence of Planet-Wide Groundwater System on Mars". Journal of Geophysical Research: Planets 124 (2): 374–395. doi:10.1029/2018JE005802. PMID 31007995. Bibcode: 2019JGRE..124..374S. 
  11. ↑ Burns, Roger G (1993). "Rates and mechanisms of chemical weathering of ferromagnesian silicate minerals on Mars". Geochimica et Cosmochimica Acta 57 (19): 4555–4574. doi:10.1016/0016-7037(93)90182-V. Bibcode: 1993GeCoA..57.4555B. 
  12. ↑ Burns, Roger G.; Fisher, Duncan S. (1993). "Rates of Oxidative Weathering on the Surface of Mars". Journal of Geophysical Research 98 (E2): 3365–3372. doi:10.1029/92JE02055. Bibcode: 1993JGR....98.3365B. 
  13. ↑ Hurowitz, J. A.; Fischer, W. W.; Tosca, N. J.; Milliken, R. E. (2010). "Origin of acidic surface waters and the evolution of atmospheric chemistry on early Mars". Nat. Geosci. 3 (5): 323–326. doi:10.1038/ngeo831. Bibcode: 2010NatGe...3..323H. https://authors.library.caltech.edu/18444/2/ngeo831-s1.pdf. 
  14. ↑ Andrews-Hanna, Jeffrey C.; Lewis, Kevin W. (2011). "Early Mars hydrology: 2. Hydrological evolution in the Noachian and Hesperian epochs". Journal of Geophysical Research 116 (E2): E02007. doi:10.1029/2010JE003709. Bibcode: 2011JGRE..116.2007A. 
  15. ↑ Andrews-Hanna, J., K. Lewis. 2011. Early Mars hydrology:2. Hydrological evolution in the Noachian and Hesperian epochs. JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 116, E02007, doi:10.1029/2010JE003709.
  16. ↑ Schwenzer, S. P., et al. 2016. Fluids during diagenesis and sulfate vein formation in sediments at Gale Crater, Mars, Meteorit. Planet. Sci., 51(11), 2175–2202, doi:10.1111/maps.12668.
  17. ↑ L'Haridon, J., N. Mangold, W. Rapin, O. Forni, P.-Y. Meslin, E. Dehouck, M. Nachon, L. Le Deit, O. Gasnault, S. Maurice, R. Wiens. 2017. Identification and implications of iron detection within calcium sulfate mineralized veins by ChemCam at Gale crater, Mars, paper presented at 48th Lunar and Planetary Science Conference, The Woodlands, Tex., Abstract 1328.
  18. ↑ Lanza, N. L., et al. 2016. Oxidation of manganese in an ancient aquifer, Kimberley formation, Gale crater, Geophys. Res. Lett., 43, 7398–7407, doi:10.1002/2016GL069109.
  19. ↑ Frydenvang, J., et al. 2017. Diagenetic silica enrichment and late-stage groundwater activity in Gale crater, Mars, Gale, Mars, Geophys. Res. Lett., 44, 4716–4724, doi:10.1002/2017GL073323.
  20. ↑ Yen, A. S., et al. 2017. Multiple stages of aqueous alteration along fractures in mudstone and sandstone strata in Gale Crater, Mars, Earth Planet. Sci. Lett., 471, 186–198, doi:10.1016/j.epsl.2017.04.033.
  21. ↑ Nachon, M., et al. 2014. Calcium sulfate veins characterized by ChemCam/Curiosity at Gale crater, Mars, J. Geophys. Res. Planets, 119, 1991–2016, doi:10.1002/2013JE004588
  22. ↑ Edgett, Kenneth S. (2005). "The sedimentary rocks of Sinus Meridiani: Five key observations from data acquired by the Mars Global Surveyor and Mars Odyssey orbiters". The Mars Journal 1: 5–58. doi:10.1555/mars.2005.0002. Bibcode: 2005IJMSE...1....5E. 
  23. ↑ Malin, M. P.; Edgett, K. S. (2000). "Ancient sedimentary rocks of early Mars". Science 290 (5498): 1927–1937. doi:10.1126/science.290.5498.1927. PMID 11110654. Bibcode: 2000Sci...290.1927M. 
  24. ↑ Fassett, Caleb I.; Head, James W. (2007). "Layered mantling deposits in northeast Arabia Terra, Mars: Noachian-Hesperian sedimentation, erosion, and terrain inversion". Journal of Geophysical Research 112 (E8): E08002. doi:10.1029/2006JE002875. Bibcode: 2007JGRE..112.8002F. 
  25. ↑ Fergason, R. L.; Christensen, P. R. (2008). "Formation and erosion of layered materials: Geologic and dust cycle history of eastern Arabia Terra, Mars". Journal of Geophysical Research 113 (E12): 12001. doi:10.1029/2007JE002973. Bibcode: 2008JGRE..11312001F. 
  26. ↑ Lewis, K. W.; Aharonson, O.; Grotzinger, J. P.; Kirk, R. L.; McEwen, A. S.; Suer, T.-A. (2008). "Quasi-Periodic Bedding in the Sedimentary Rock Record of Mars". Science 322 (5907): 1532–5. doi:10.1126/science.1161870. PMID 19056983. Bibcode: 2008Sci...322.1532L. https://authors.library.caltech.edu/12528/2/LEWsci08supp.pdf. 
  27. ↑ Lewis, K. W., O. Aharonson, J. P. Grotzinger, A. S. McEwen, and R. L. Kirk (2010), Global significance of cyclic sedimentary deposits on Mars, Lunar Planet. Sci., XLI, Abstract 2648.
  28. ↑ Habermehl, M. A. (1980). "The Great Artesian Basin, Australia". J. Austr. Geol. Geophys 5: 9–38. 
  29. ↑ 29.0 29.1 ESA Staff (28 February 2019). "First Evidence of "Planet-Wide Groundwater System" on Mars Found". European Space Agency. https://www.esa.int/Our_Activities/Space_Science/Mars_Express/First_evidence_of_planet-wide_groundwater_system_on_Mars. 
  30. ↑ 30.0 30.1 Houser, Kristin (28 February 2019). "First Evidence of "Planet-Wide Groundwater System" on Mars Found". Futurism.com. https://futurism.com/the-byte/mars-groundwater-system-planet-wide. 
  31. ↑ Morgan, A.M.; Howard, A.D.; Hobley, D.E.J.; Moore, J.M.; Dietrich, W.E.; Williams, R.M.E.; Burr, D.M.; Grant, J.A.; Wilson, S.A.; Matsubara, Y. (2014). "Sedimentology and climatic environment of alluvial fans in the martian Saheki crater and a comparison with terrestrial fans in the Atacama Desert". Icarus. 229: 131–156. Bibcode:2014Icar..229..131M. doi:10.1016/j.icarus.2013.11.007.
  32. ↑ Andrews-Hanna, Jeffrey C.; Zuber, Maria T.; Arvidson, Raymond E.; Wiseman, Sandra M. (2010). "Early Mars hydrology: Meridiani playa deposits and the sedimentary record of Arabia Terra". Journal of Geophysical Research 115 (E6): E06002. doi:10.1029/2009JE003485. Bibcode: 2010JGRE..115.6002A. 
  33. ↑ Arvidson, R. E.; Poulet, F.; Morris, R. V.; Bibring, J.-P.; Bell, J. F.; Squyres, S. W.; Christensen, P. R.; Bellucci, G. et al. (2006). "Nature and origin of the hematite-bearing plains of Terra Meridiani based on analyses of orbital and Mars Exploration rover data sets". Journal of Geophysical Research 111 (E12): n/a. doi:10.1029/2006JE002728. Bibcode: 2006JGRE..11112S08A. https://authors.library.caltech.edu/34879/1/2006JE002728.pdf. 
  34. ↑ Baker, V. R. (1982), The Channels of Mars, 198 pp., Univ. of Tex. Press
  35. ↑ "Opportunity Rover Finds Strong Evidence Meridiani Planum Was Wet". http://marsrovers.jpl.nasa.gov/newsroom/pressreleases/20040302a.html. 
  36. ↑ Grotzinger, J.P.; Arvidson, R.E.; Bell, J.F.; Calvin, W.; Clark, B.C.; Fike, D.A.; Golombek, M.; Greeley, R. et al. (2005). "Stratigraphy and sedimentology of a dry to wet eolian depositional system, Burns formation, Meridiani Planum, Mars". Earth and Planetary Science Letters 240 (1): 11–72. doi:10.1016/j.epsl.2005.09.039. Bibcode: 2005E&PSL.240...11G. 
  37. ↑ McLennan, S.M.; Bell, J.F.; Calvin, W.M.; Christensen, P.R.; Clark, B.C.; De Souza, P.A.; Farmer, J.; Farrand, W.H. et al. (2005). "Provenance and diagenesis of the evaporite-bearing Burns formation, Meridiani Planum, Mars". Earth and Planetary Science Letters 240 (1): 95–121. doi:10.1016/j.epsl.2005.09.041. Bibcode: 2005E&PSL.240...95M. 
  38. ↑ Squyres, Steven W.; Knoll, Andrew H. (2005). "Sedimentary rocks at Meridiani Planum: Origin, diagenesis, and implications for life on Mars". Earth and Planetary Science Letters 240 (1): 1–10. doi:10.1016/j.epsl.2005.09.038. Bibcode: 2005E&PSL.240....1S. 
  39. ↑ Karsenti, E.; Vernos, I. (Oct 2001). "The mitotic spindle: a self-made machine.". Science 294 (5542): 543–7. doi:10.1126/science.1063488. PMID 11641489. Bibcode: 2001Sci...294..543K. 
  40. ↑ M. Wiseman, J. C. Andrews-Hanna, R. E. Arvidson, J. F. Mustard, K. J. Zabrusky DISTRIBUTION OF HYDRATED SULFATES ACROSS ARABIA TERRA USING CRISM DATA: IMPLICATIONS FOR MARTIAN HYDROLOGY. 42nd Lunar and Planetary Science Conference (2011) 2133.pdf
  41. ↑ Murchie, Scott; Roach, Leah; Seelos, Frank; Milliken, Ralph; Mustard, John; Arvidson, Raymond; Wiseman, Sandra; Lichtenberg, Kimberly et al. (2009). "Evidence for the origin of layered deposits in Candor Chasma, Mars, from mineral composition and hydrologic modeling". Journal of Geophysical Research 114 (E12): E00D05. doi:10.1029/2009JE003343. Bibcode: 2009JGRE..114.0D05M. 
  42. ↑ Gendrin, A.; Mangold, N; Bibring, JP; Langevin, Y; Gondet, B; Poulet, F; Bonello, G; Quantin, C et al. (2005). "Sulfates in Martian Layered Terrains: The OMEGA/Mars Express View". Science 307 (5715): 1587–91. doi:10.1126/science.1109087. PMID 15718429. Bibcode: 2005Sci...307.1587G. 
  43. ↑ Roach, Leah H.; Mustard, John F.; Swayze, Gregg; Milliken, Ralph E.; Bishop, Janice L.; Murchie, Scott L.; Lichtenberg, Kim (2010). "Hydrated mineral stratigraphy of Ius Chasma, Valles Marineris". Icarus 206 (1): 253–268. doi:10.1016/j.icarus.2009.09.003. Bibcode: 2010Icar..206..253R. 
  44. ↑ 44.0 44.1 44.2 Salese, Francesco; Pondrelli, Monica; Neeseman, Alicia; Schmidt, Gene; Ori, Gian Gabriele (2019). "Geological Evidence of Planet-Wide Groundwater System on Mars". Journal of Geophysical Research: Planets 124 (2): 374–395. doi:10.1029/2018JE005802. PMID 31007995. Bibcode: 2019JGRE..124..374S. 
  45. ↑ David, Leonard (2019-02-19). "Mars: Planet-Wide Groundwater System – New Geological Evidence" (in en-US). https://www.leonarddavid.com/planet%e2%80%90wide-groundwater-system-on-mars-new-geological-evidence/. 
  46. ↑ "First Evidence of a Planet-wide Groundwater System on Mars - Astrobiology". 28 February 2019. http://astrobiology.com/2019/02/first-evidence-of-a-planet-wide-groundwater-system-on-mars.html. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Groundwater_on_Mars&oldid=3346403"